3. Квадратичная зависимость.

Функция квадратичной зависимости представляет собой зависимость типа у = а·х² + b·х + с

По сравнению с предыдущими функциями, за счет изменения параметров а и b, можно значительно расширить спектр предоставления опытных данных. Для оценки пригодности квадратичной зависимости используют метод разделённых разностей.

Порядок расчёта:

1. Определяем последовательно разности экспериментальных данных

Δх_i = x_i+1 - x_i

Δy_i = y_i+1 - y_i

2. Определяем разделённые разности первого порядка .

3. Определяем разделённые разности второго порядка:

Применение квадратичной функции для решения задач возможно в том случае, если отклонение разделённых разностей второго порядка от их среднего находится в пределах 0,05 ÷ 0,1.

N – число измерений

N = 7

Для удобства составим таблицу значений.

Таблица 3.

Вычисляем среднее значение разностей второго порядка:

Проверим отклонение крайних значений:

Отклонения не попадают в интервал, значит квадратичная зависимость не подходит.

2. Коэффициент парной корреляции и уравнение регрессии.

С помощью этого метода можно установить статистическую связь между выходными параметрами сложной системы. Статистическая связь между двумя параметрами устанавливается на основе определения парной корреляции. Его значение лежит в интервале от -1 до 1.

(1)

S – среднеквадратичное отклонение

x, y – средние

Упрощённый расчёт:

(2)

x, y – первый и второй параметры, между которыми устанавливается корреляция

n – число опытов по определению x и y

- средние арифметические

Подставим выражения (3) – (5) в уравнение (2).

Для расчёта по упрощённым формулам целесообразно заполнить таблицу 4.

Таблица 4.

Подсчитаем коэффициент парной корреляции:

Установим статистическую значимость коэффициента парной корреляции. С этой целью по выбранному уровню доверительной вероятности α (0,95 ÷ 0,99) и числу степеней свободы f = n-2 определяем критическое значение коэффициента r_кр. В случае, если абсолютная величина коэффициента не меньше критического, то линейная связь между параметрами является статически значимой. В противоположном случае, связь статически не значима, и, следовательно, необходимо переходить к более сложным математическим зависимостям.

f = 7 – 2 = 5

Для α = 0,95 r_кр = 0,754

Для α = 0,99 r_кр = 0,874

Так как r(x,y) > r_кр, то линейная связь является статически значимой. Поэтому найдём коэффициенты уравнения регрессии.

И построим график функции: у = 0,04·х +0.8

3. Метод средних

Для определения числовых параметров необходимо задать n точек с координатами (x_i; y_i). Для выбранного вида функции y = f(x, a₁, a₂, … , a_m) необходимо вычислить значения коэффициентов от a₁ до a_m. Задача вычисления коэффициентов решается в том случае, если n > m.

Т.к вид функции выбирается с определёнными допущениями, между расчётными и экспериментальными значениями, существуют отклонения

Ε_i = y_i – f(x, a₁, …, a_m)

Основное условие определения коэффициентов a₁…a_m – обеспечение минимально возможных значений отклонений.

Метод средних основан на расчёте отклонений от расчетной кривой. Отклонение – это расстояние между результатом измерения и расчётной кривой.

ε₃

ε₁

ε₂

По методу средних, условием определения числовых параметров функции, является равенство нулю алгебраической суммы отклонений.

Порядок определения параметров:

N = n₁ + n₂ + … + n_m

N отклонений разбивают на группы по числу определяемых параметров m. Получаем систему уравнений. Число отклонений в каждой группе должно быть приблизительно одинаково. Сумму отклонений в каждой группе приравнивают к нулю.

Е_i = у – (а·х² + b·х + с)

Е₁ = 12 – (а·(100)² + b·100 + с)

Е₂ = 9 – (а·(200)² + b·200 + с)

Е₃ = 8 – (а·(300)² + b·300 + с)

Е₄ = 14 – (а·(500)² + b·500 + с)

Е₅ = 20 – (а·(600)² + b·600 + с)

Е₆ = 30 – (а·(700)² + b·700+ с)

Е₇ = 40 – (а·(800)² + b·800 + с)

Составляем систему уравнений

Выразим из первого уравнения коэффициент а и подставим во второе и третье уравнения:

Преобразовав эту систему получим:

Выразим из первого уравнения коэффициент b и подставим во второе. Затем найдём коэффициент с.

Затем находим оставшиеся коэффициенты a и b. Получаем, что

Следовательно, искомая функция выглядит следующим образом:

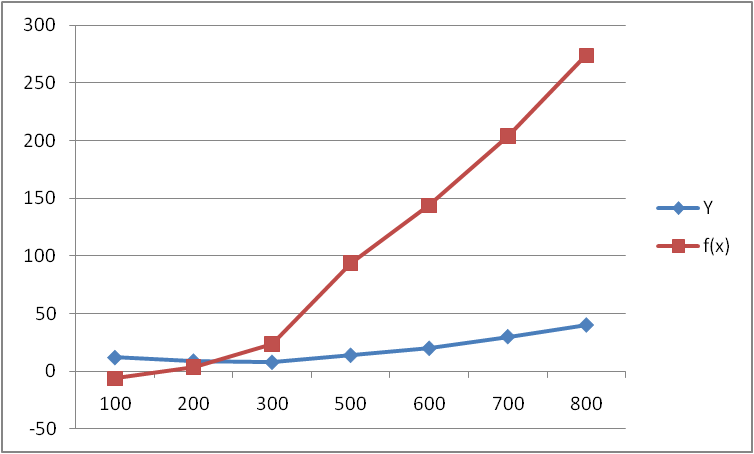
у = 0.0005 ·х² – 0.05·х –6.26

Для наглядности построим график этой функции и отметим исходные семь точек.