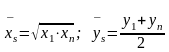ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«МАТИ - РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ

УНИВЕРСИТЕТ им. К.Э.ЦИОЛКОВСКОГО» (МАТИ)

____________________________________________________________

Кафедра "Материаловедение и технология обработки материалов"

Курсовая работа

по дисциплине «Моделирование и оптимизация материалов

и покрытий»

Студент: Ядгаров А.И.

Группа: 4МЕД – 4ДБ – 041.

Преподаватель: Фёдорова Л. В.

Москва

2013

Содержание:

Задание	3
Построение статистических моделей по результатам пассивного эксперимента.	4
Метод сравнения средних	4
Функция одного аргумента с двумя числовыми параметрами	5
Функция одного аргумента с тремя числовыми параметрами	7
Квадратичная зависимость	9
Коэффициент парной корреляции и уравнение регрессии	11
Метод средних	14
Метод Лагранжа	17
Построение статистических моделей по результатам активного эксперимента.	19
Метод планирования эксперимента и регрессионный анализ результатов.	19
Обобщённая оптимизация.	23

1. Задание:

1. Задание:

Часть 1:

1. Методом сравнения средних подобрать вид функции для данной выборки.

2. Определить коэффициент парной корреляции и определить уравнение регрессии.

3. Методом средних определить вид функции и квадратичной функции.

4. Методом Лагранжа определить вид полинома второй степени.

Таблица 1.

Температура нагрева	100	200	300	500	600	700	800
δ,%	12	9	8	14	20	30	40

Часть 2:

1. Построить уравнение для определения σ_в (y) в зависимости от состава сплава системы Ti-Mo-Zr-Si: Mo (x₁) = 3-5%, Zr (x₂) = 2-4%,Si(x₃)=0,2-0,6% по результатам ПФЭ типа 2³. В первом опыте принять нижний уровень факторов, результаты опытов в матрице (σ_в): 770, 935, 1030,1190, 920, 1080,1175, 1340.Проверить опыты с нулевым уровнем: 1055, 1050, 1060, 1054, 1065. Проверить воспроизводимость эксперимента, определить коэффициенты линейного уравнения:

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃+ b₂₃x₂x₃,

провести регрессионный анализ полинома.

2. Выбрать тип стали без термической обработки для обеспечения требуемых характеристик: σ_в>700МПа; δ=18-20%; T(полухрупкости)=-50÷-100^оС Таблица 1.2.

	σв МПа	δ %	Т оС
1	720	19	-100
2	750	19,5	-70
3	790	20	-50
4	820	18	-80
5	880	19	-90

2. Построение статистических моделей по результатам пассивного эксперимента.

   1. Метод сравнения средних

С помощью метода сравнения средних решаются 2 задачи:

• Выбор функции.

• Определение числовых коэффициентов выбранных функций.

Оценка пригодности выбранной функции проводится методом сравнения среднего экспериментального результата (y_s) в пределах x₁ ÷ x_n с соответствующим средним арифметическим для набора данных значением для анализированной функции.

Для различных функций среднее арифметическое вычисляется по различным уравнениям.

Если y_s мало отличается от , то можно использовать для данной выборки данную функцию.

Обычно используют функции:

1. Линейная: у = а + b·х

2. Степенная: у = а·х^b

3. Показательная: у = а·b^х или у = а·е^b·х

4. Гиперболическая: у = а + b/х

5. Логарифмическая: у = а + b·lg(х)

Для каждой из этих функций существуют следующие формулы для определения среднего значения х и у.

1. 

2. 

3. 

4. 

5. 

Порядок выбора вида функции включает:

1. Расчёт среднего значения для предварительного выбора функции.

2. По найденному определяется y_s. Если соответствует какое-либо х_i, то = х_i, тогда y_s = у_i. Если ≠ х_i, то y_s считаем методом линейного интерполирования:

Чтобы произвести сравнение двух средних значений y_s, необходимо вычислить относительное отклонение этих значений φ. Величина отклонений не должна превышать 0,03 ÷ 0,05.

Сначала проверим функции одного аргумента с двумя числовыми параметрами, затем функции одного аргумента с тремя числовыми параметрами.