Но стержневые (ключевые) теоремы

8) теорема о производной: f(t) _=^ F(p)   _=^ pF(p) – f(0);

9) теорема об интеграле:  _=^  ,

они алгебраизируют систему дифференциальных уравнений.

Некоторые типовые преобразования Лапласа

В справочниках табулировано большое число функций и их изменений.

24. Законы Ома и Кирхгофа в операторной форме

Р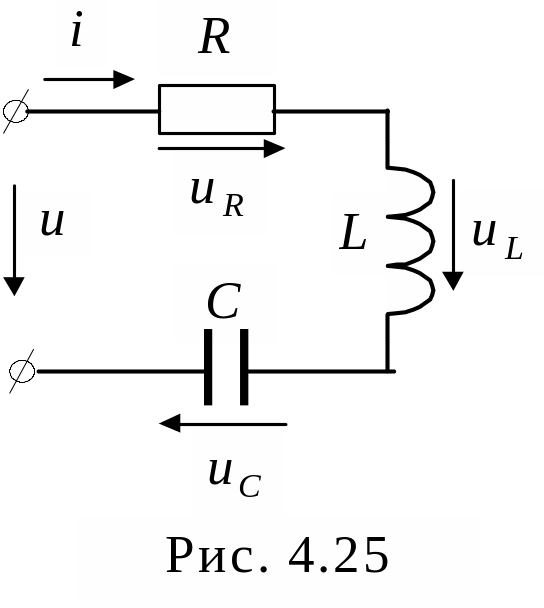 ассмотрим цепь (рис. 4.25). II закон Кирхгофа во временной области (для оригиналов):

. (4.29)

К уравнению (4.29) применим преобразование Лапласа. Преобразование Лапласа является линейным, поэтому изображение суммы равно сумме изображений:

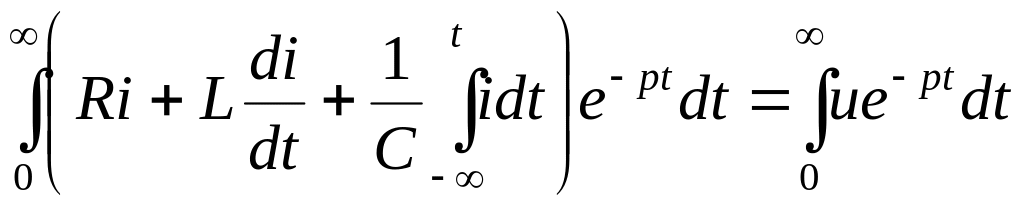. (4.30)

Каждое слагаемое уравнения (4.30) заменим операторным изображением:

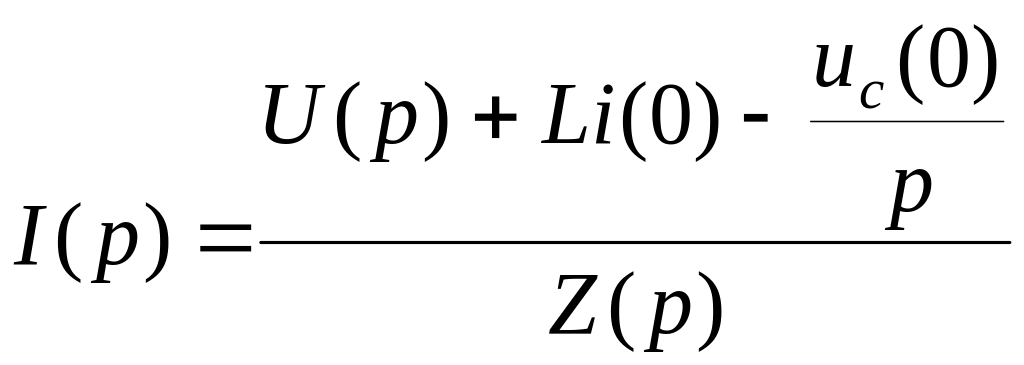, (4.31)

где  – операторное сопротивление;

 – операторная ЭДС, учитывающая ненулевой запас энергии магнитного поля W_м в индуктивности (по току i_L(0));

 – операторная ЭДС, учитывающая ненулевой запас энергии электрического поля W_эл в емкости (по напряжению u_C(0))/

При нулевых начальных условиях (аналогично цепям постоянного тока).

По I закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю . Применим преобразование Лапласа к этому уравнению и воспользуемся тем, что изображение суммы равно сумме изображений

. (4.32)

Уравнение (4.32) выражает собой I закон Кирхгофа в операторной форме, аналогично выражению для цепей постоянного тока.

Для любого замкнутого контура электрической цепи можно составить уравнение по II закону Кирхгофа . Применим преобразование Лапласа

. (4.33)

Уравнение (4.33) представляет собой математическую запись II закона Кирхгофа в операторной форме, уравнение (4.34) представляет собой модификацию (4.33)

. (4.34)

Аналог в цепях постоянного тока .

При нулевых начальных условиях просматривается полная аналогия с цепями постоянного тока, при ненулевых появляются отличия, заключающиеся в необходимости введения операторных ЭДС, учитывающих и отображающих ненулевой запас энергии магнитного поля W_м в индуктивности и энергии электрического поля W_эл в емкости.

Отсюда важный вывод: весь расчетный аппарат работает и при анализе переходных процессов, только в операторной форме. При этом необходимо учесть операторные ЭДС.

25. Эквивалентные операторные схемы

П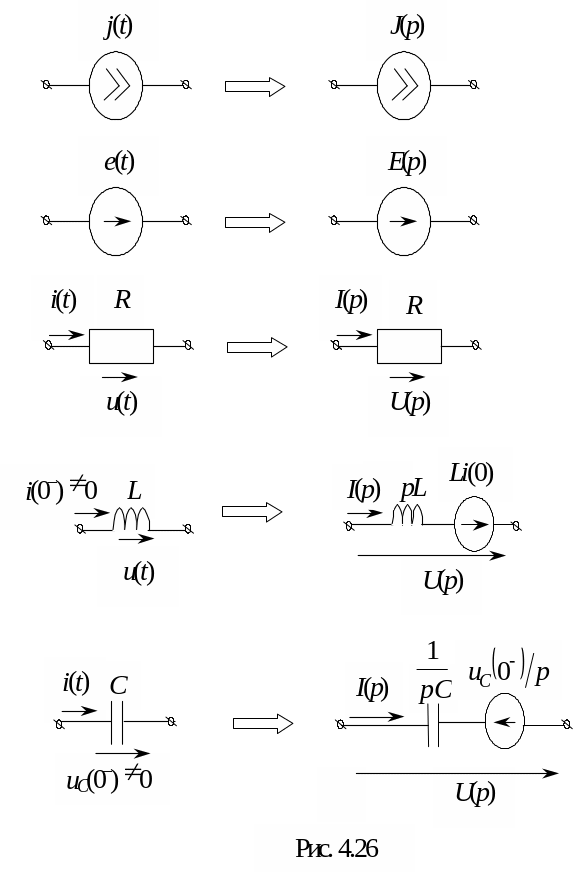 ри расчете переходных процессов операторным методом удобно составить предварительно операторную схему. В каждой ветви с параметрами R, L, C должны быть при ненулевых начальных условиях учтены две дополнительные внутренние ЭДС Li(0) и u_C(0)/p. На рис. 4.26 показаны переходы от элементов с мгновенными значениями токов и напряжений к элементам операторной схемы.

26. Порядок расчета переходных процессов операторным методом

1. Анализ независимых начальных условий (для этого необходимо рассчитать режим в t = 0^–).

2. Составление эквивалентной операторной схемы.

3. Расчет операторной схемы любым расчетным методом в операторной форме, привести изображение X(p) искомой величины к виду рациональной дроби.

4. Определение оригинала x(t) по X(p), т.е. обратный переход.

27. Нахождение оригинала по изображению

При расчете переходных процессов операторным методом необходимо не только находить изображение функций, их производных и интегралов, но и решать обратную задачу – находить функции (оригиналы) по их изображениям. Существуют следующие способы решения этой проблемы:

1. Использование обратного преобразования Лапласа

, (4.35)

которое представляет собой решение интегрального уравнения (4.27) относительно неизвестной функции f(t) и может быть получено методами теории функций комплексного переменного. Интеграл (4.35) вычисляется по прямой на плоскости комплексного переменного p, параллельной мнимой оси и расположенной правее всех особенностей (в частности, простых и кратных полюсов) функции F(p). Такой способ в прикладных задачах электротехники не используется.

2. Табличный метод. Подробные таблицы оригиналов и соответствующих им изображений приводятся в математических и электротехнических справочниках. При использовании этого способа возникают трудности, связанные с распознаванием и сведением функций к табличному виду.

3. Использование теоремы о вычетах или теоремы разложения.

Для каждой функции времени, входящей в уравнение Кирхгофа, описывающего расчетную цепь, устанавливается в соответствие операторное изображение, после чего система линейных дифференциальных уравнений переписывается в виде системы алгебраических уравнений (также получаем операторную схему замещения). Система алгебраических уравнений рассчитывается относительно операторного изображения искомой величины, по которому с помощью теоремы разложения находится оригинал.

Теорема разложения имеет две модификации в зависимости от операторного изображения искомой величины:

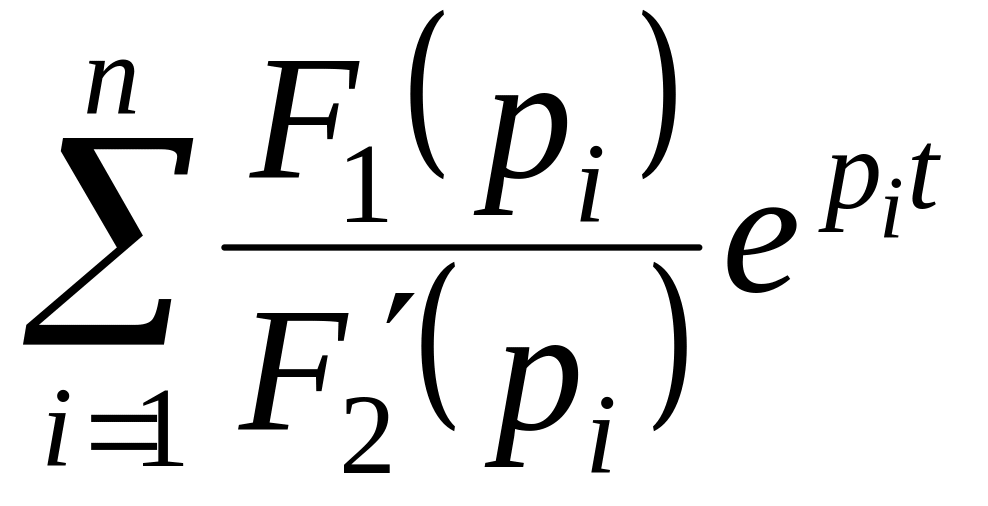1)  _=^  , (4.31)

где n – порядок цепи,

p_i – простые корни характеристического уравнения N(p) = 0;

.

2)  _=^  , (4.32)

где p_i – корни характеристического уравнения F₃(p) = 0.

В этом случае знаменатель имеет один нулевой корень, на это указывает наличие в составе знаменателя множителя p. Теорема разложения в форме (4.32) соответствует сигналам, имеющим принужденную составляющую.

Если уравнение F₂(p) = 0 имеет комплексные сопряженные корни и , то достаточно вычислить слагаемое сумм (4.31) или (4.32) только для корня , а для корня взять значение, сопряженное этому слагаемому, т.е.

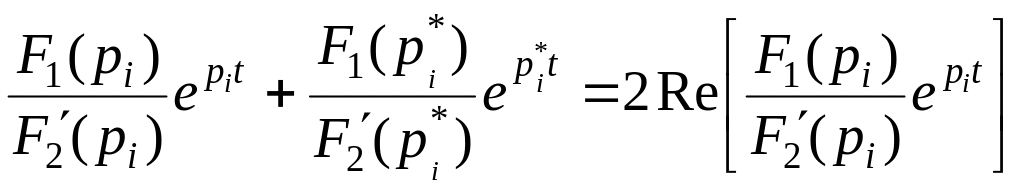_=^ (4.33)

или

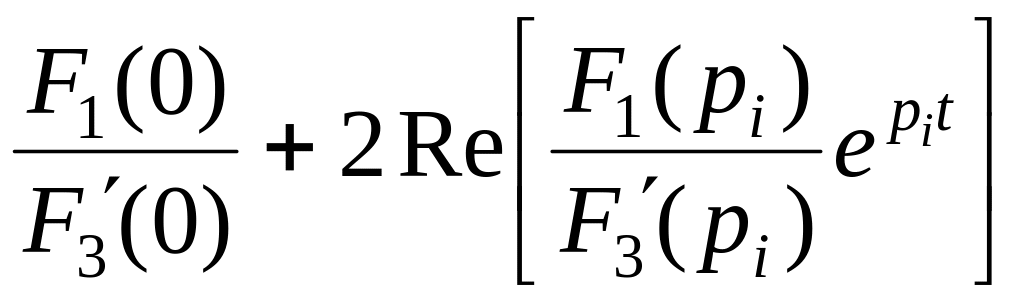 _=^  . (4.34)

Если среди корней многочлена F₂(p) = 0 есть q простых корней (p₁, p₂, …, p_q), корень p_r кратности r и корень p_s кратности s, то можно записать теорему разложения с двойной суммой в правой части (одна сумма – по числу корней, а вторая – для каждого корня по порядку его кратности):

 _=^ 

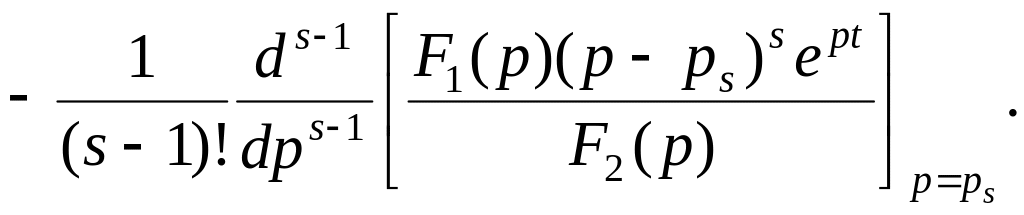(4.35)

Если нужно вычислить начальное (при t = 0⁺) и установившееся (при t = ) значения оригинала, т.е. f(0⁺) и f(), то можно воспользоваться формулами (4.31) и (4.32). Однако начальное и установившееся значения оригинала в случае, если установившийся процесс непериодический, определяются достаточно просто по так называемым предельным соотношениям:

(4.36)

и

. (4.37)

Рассмотрим специфические особенности применения метода.

Пример 1. Рассмотрим заряд конденсатора при подключении RC–цепи на постоянное напряжение (рис. 4.26, а). Определим закон изменения в переходном режиме.

Цепь с нулевыми начальными условиями. Соответствующая операторная схема замещения представлена на рис. 4.26, б.

Операторное изображение напряжения на конденсаторе определим по закону Ома:

Изображение тока в операторной схеме замещения

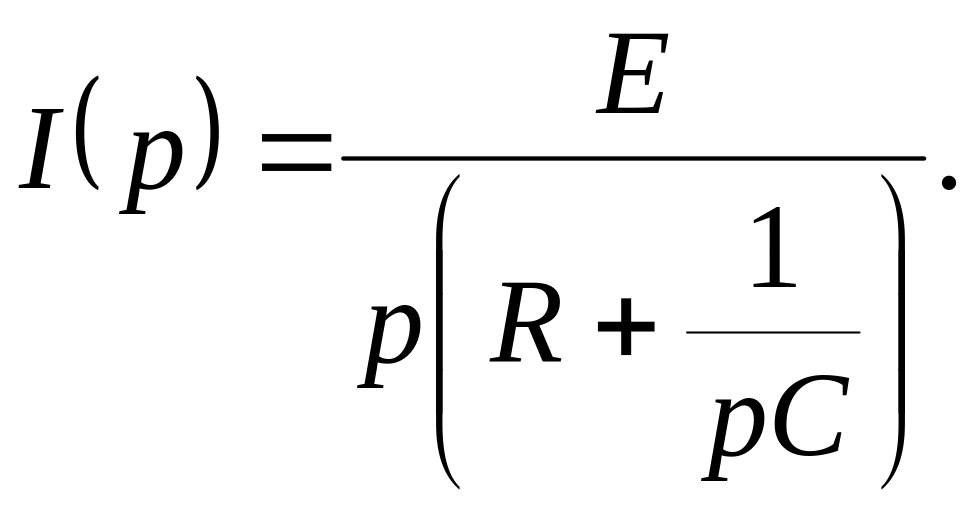
Д ля отыскания воспользуемся теоремой разложения:

 _=^  .

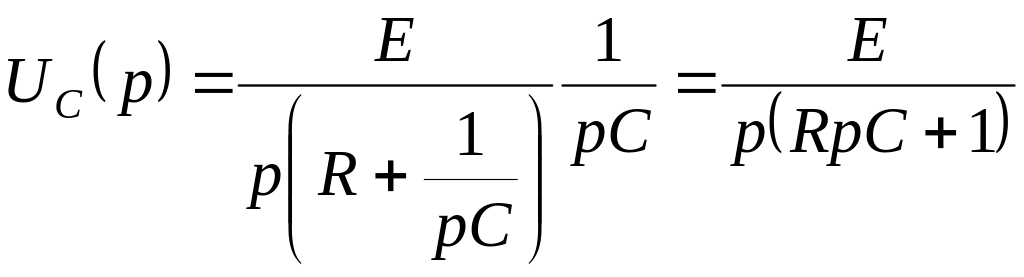Используя предельные соотношения, определим соответственно начальное и установившееся значения напряжения на конденсаторе:

Аналогичные значения будут получены по формуле, описывающей закон изменения в переходном режиме

и

.

Пример 2. Найти напряжение на емкости в цепи (рис. 4.27), подключенной к источнику постоянного напряжения U = 4 B. Параметры элементов электрической цепи приведены на рисунке.

1. Анализ независимых начальных условий (докоммутационный режим)

2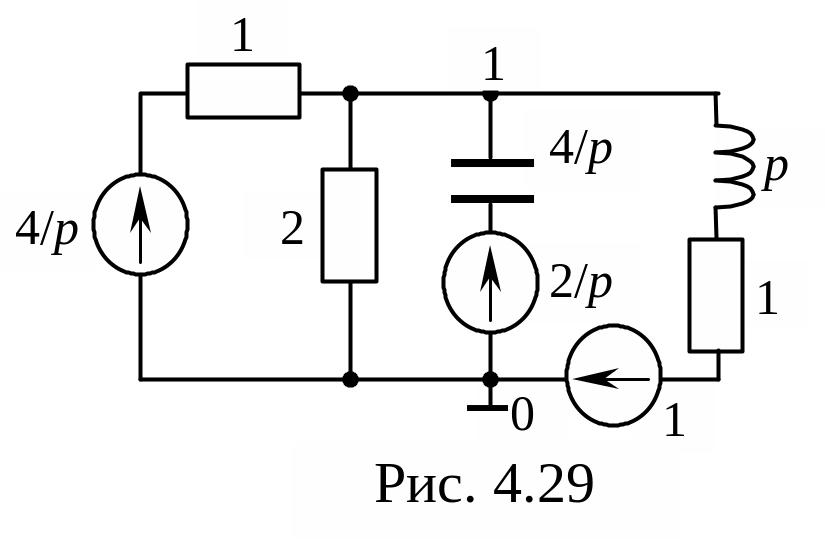 . Эквивалентная операторная схема представлена на рис. 4.29.

Операторные сопротивления:

Операторные ЭДС:

3. Расчет эквивалентной операторной схемы методом узловых потенциалов:

.

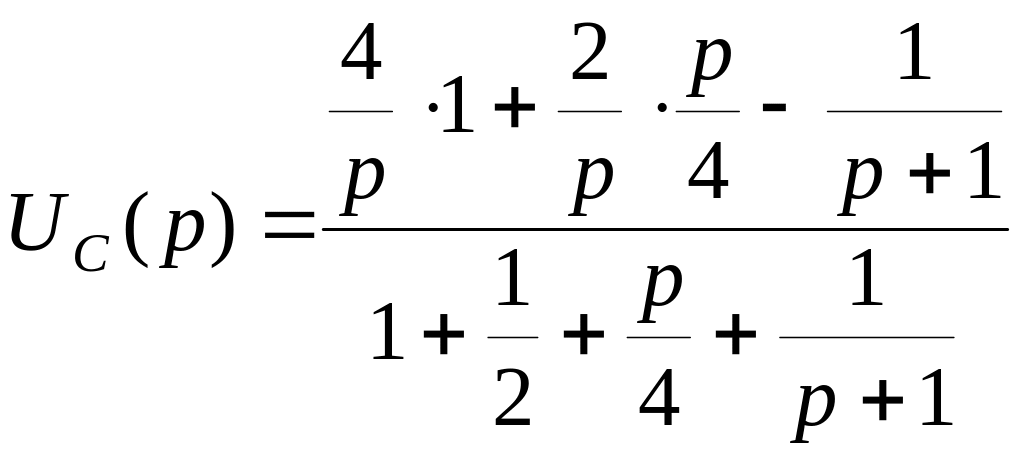После необходимых преобразований получим

.

4. Для отыскания воспользуемся теоремой разложения:

 _=^  ,

здесь ,

,

Таким образом,

.

Окончательно

.