
- •1. Классификация четырехполюсников
- •2. Основные уравнения четырехполюсников
- •3 . Режим обратного питания четырехполюсников
- •4. Определение а–параметров с помощью режимов короткого замыкания и холостого хода
- •5. Нагрузочный режим четырехполюсника как результат наложения режимов холостого хода и короткого замыкания
- •6. Эквивалентные схемы замещения четырехполюсника
- •7. Симметричный четырехполюсник
- •8. Передаточные функции четырехполюсника
- •9. Каскадное соединение
- •1 0. Параллельное соединение
- •11. Последовательное соединение
6. Эквивалентные схемы замещения четырехполюсника
Л юбой
четырехполюсник можно свести к
сопротивлениям или проводимостям,
соединенным по Т– или П–образной схеме
(рис. 3.5). Эквивалентной схемой замещения
реального четырехполюсника называется
простейший трехэлементный четырехполюсник
(Т– или П–образный), имеющий такие же
юбой
четырехполюсник можно свести к
сопротивлениям или проводимостям,
соединенным по Т– или П–образной схеме
(рис. 3.5). Эквивалентной схемой замещения
реального четырехполюсника называется
простейший трехэлементный четырехполюсник
(Т– или П–образный), имеющий такие же
![]() или A–параметры,
как и заданный четырехполюсник.
или A–параметры,
как и заданный четырехполюсник.
Три сопротивления Т– или П–схем должны быть рассчитаны с учетом того, что схема замещения должна обладать такими же А-параметрами, какими обладает заменяемый ей четырехполюсник.
Выразим и Т–образной схемы через , , используя уравнения, составленные по законам Кирхгофа:
![]() (3.18)
(3.18)
Подставляя в выражение для определения и группируя однородные члены, получим
![]()
![]() .
.
С другой стороны для данной схемы справедлива общая запись уравнений четырехполюсника в А–параметрах:
![]()
![]() .
.
Приравняв коэффициенты при и , получим А–параметры как функции параметров Т-образной схемы замещения:
![]() (3.19)
(3.19)
Проведя аналогичные действия, можно получить подобные соотношения для П–образной схемы четырехполюсника:
![]() (3.20)
(3.20)
Два четырехполюсника эквивалентны, если у них равны А–параметры. Это следует из уравнений (3.9). Следовательно, если известны А–параметры какого-то четырехполюсника, то его можно заменить на эквивалентную ему Т– или П–образную схемы замещения, если определить параметры этих схем замещения в выражениях (3.19) и (3.20). При этом для Т–образной схемы замещения
![]() . (3.21)
. (3.21)
Параметры элементов П–образной схемы замещения
![]() . (3.22)
. (3.22)
7. Симметричный четырехполюсник
Встречаются
такие электрические схемы, у которых
наблюдается симметрия параметров
относительно входных и выходных выводов.
В эквивалентных схемах замещения это
приводит к следующему: для Т–схемы
![]() ;
для П–схемы
;
для П–схемы
![]() .
.
Тогда для Т–схемы
![]() ,
,
для П–схемы
![]() .
.
Следовательно,
для симметричного четырехполюсника
![]() .
Таким образом, симметричный четырехполюсник
характеризуется двумя независимыми
параметрами.
.
Таким образом, симметричный четырехполюсник
характеризуется двумя независимыми
параметрами.
8. Передаточные функции четырехполюсника
Токи
и напряжения могут быть выражены через
токи и напряжения со стороны входа и
выхода с помощью передаточных коэффициентов
![]() и
и
![]() .
Передаточная функция – это отношение
комплексных амплитуд или комплексных
действующих значений электрической
величины на выходе и входе четырехполюсника
при заданном режиме нагрузки. Выразив
эти коэффициенты через А–параметры,
получим коэффициент
передачи (или передаточную функцию) по
напряжению
.
Передаточная функция – это отношение
комплексных амплитуд или комплексных
действующих значений электрической
величины на выходе и входе четырехполюсника
при заданном режиме нагрузки. Выразив
эти коэффициенты через А–параметры,
получим коэффициент
передачи (или передаточную функцию) по
напряжению
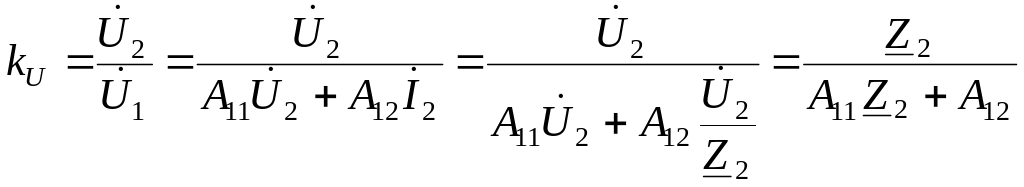 (3.47)
(3.47)
и коэффициент передачи по току
![]() . (3.48)
. (3.48)
Используются и такие передаточные функции как передаточное сопротивление
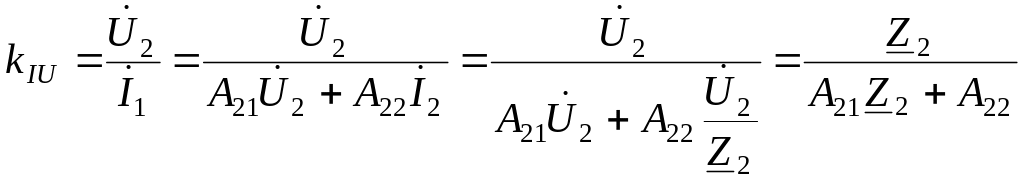
и передаточная проводимость
![]() .
.
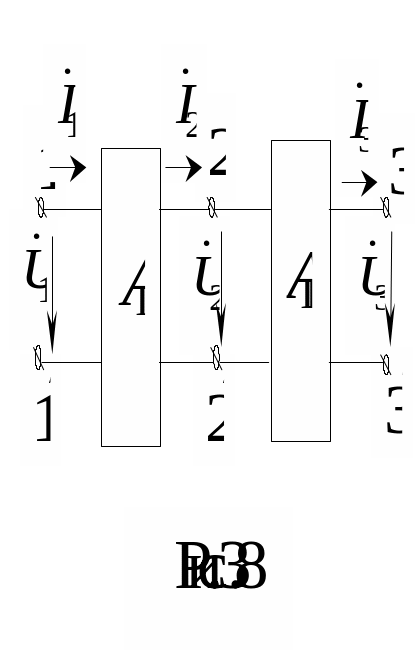
9. Каскадное соединение
Пусть в цепной схеме соединения заданы А–параметры четырехполюсника (АI) и (АII). Выразим напряжение и ток на входе четырехполюсника заданными напряжениями и токами на выходе последнего четырехполюсника (в данном случае второго). Для первого и второго четырехполюсников справедливо
![]()
 ,
(3.49)
,
(3.49)![]() (3.50)
(3.50)
Подставив
значение матрицы
![]() из (3.50) в (3.49), получим
из (3.50) в (3.49), получим
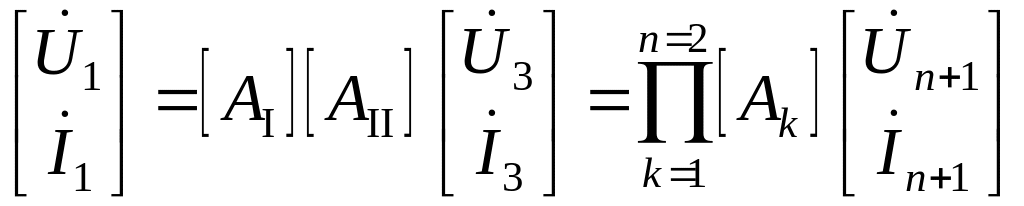 .
.
Если схема состоит из n четырехполюсников, справедливо равенство
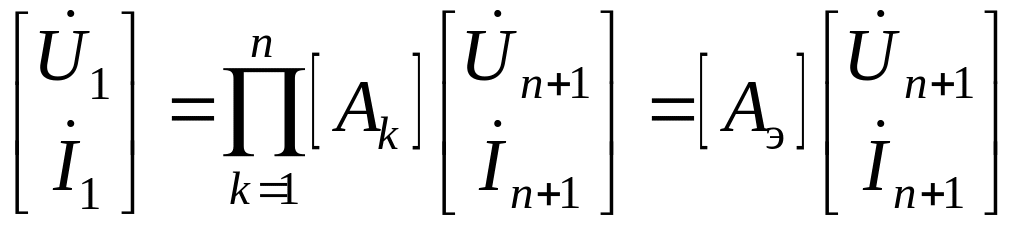 , (3.51)
, (3.51)
где
Aэ
– эквивалентная матрица, равная
произведению n
матриц,
![]() .
.
