Дифференциалдық теңдеулер

1. Дифференциалдық теңдеулер туралы түсінік

Анықтама. Тәуелсіз х айнымалы, ізделінетін функция және тәуелсіз айнымалы бойынша алынған оның туындыларын байланыстыратын

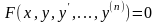(9.1)

теңдігі дифференциалдық теңдеу деп аталады.

Теңдеуге кіретін туындылардың ең жоғарғы реті теңдеудің реті деп аталады.

Егер (9.1) дифференциалдық теңдеуді ең жоғарғы туындысы арқылы шешіп,

(9.2)

түрінде жазсақ, ол қалыпты түрдегі дифференциалдық теңдеу деп аталады.

Егер дифференциалдық теңдеудегі ізделінетін функция тек қана бір айнымалыға тәуелді болса, онда ол жәй дифференциалдық теңдеу, ал бірнеше айнымалылардан тәуелді болса, онда дербес туындылы дифференциалдық теңдеу деп аталады.

Дифференциялдық теңдеуді қанағаттандыратын кез-келген функция осы теңдеудің шешімі немесе интегралы деп аталады.

Ерікті тұрақтылардың саны теңдеудің ретіне тең болатын дифференциялдық теңдеудің шешімі (егер ол бар болса) берілген дифференциялдық теңдеудің жалпы шешімі деп аталады.

Мысалы, - үшінші ретті жәй дифференциалдық теңдеу, - бірінші ретті, - бесінші ретті; ал - бірінші ретті дербес туындылы дифференциалдық теңдеу болып табылады.

Дербес шешім бір айнымалы функция болғандықтан, оның графигі дифференциялдық теңдеудің интегралдық қисығы деп аталады. Жалпы шешімге барлық интегралдық қисықтардың жалпы жиыны сәйкес келеді. Ол жалпы дифференциялдық теңдеудің интегралдық қисықтар жиынтығы деп аталады. Ал дифференциалдық теңдеудің шешімін анықтау жолы, осы теңдеуді интегралдау деп аталады.

2. Бірінші ретті дифференциалдық теңдеулер

(9.3)

түріндегі теңдеу бірінші ретті дифференциалдық теңдеу деп аталады.

(9.4)

түріндегі теңдеу бірінші ретті туындысы бойынша анықталған қалыпты түрдегі дифференциалдық теңдеу деп аталады.

Бірінші ретті туындысы бойынша анықталған қалыпты түрдегі дифференциалдық теңдеудің дифференциалдық түрде жазылуы:

,

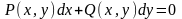мұндағы және анықталған берілген функциялар.

Дифференциалдық теңдеулерге мысалдар келтірейік:

, , , .

Анықтама. Бірінші ретті жәй дифференциалдық теңдеудің шешімі деп,

1) аралығында үзіліссіз диффренциалданатын функциясы түрінде;

2) үшін нүктесі F функциясының анықталу аймағы болатын жиынында жататын;

3) үшін тепе-теңдігі орындалатын, аралығында анықталған функцияны айтады.

Көбінесе «шешім деп, (9.4) теңдеуді қанағаттандыратын, яғни тепе-теңдікке айналдыратын функцияны айтамыз» дей береді.

Ал, шешімдерінің ішінен тек біреуін таңдап алу үшін қосымша шарттар қою арқылы, Коши есебін шешеміз: - бастапқы шарт немесе Коши шарты. (9.4) дифференциалдық теңдеудің бастапқы шартты қанағаттандыратын шешімі дербес шешім, ал есеп – Коши есебі деп аталады.

(9.4) бірінші ретті дифференциалдық теңдеудің жалпы шешімі деп,

1) кез келген С демеуші мәндері үшін функциясы (9.4) теңдеудің шешімі болып табылатын;

2) кез келген бастапқы шарт үшін, С₀ демеуші тауып, функциясы шартын қанағаттандыратындай С демеушісінен тәуелді біріне-бірі ұқсас функциялар жиынтығын айтады.

Ал, бұл теңдеулердің дербес шешімі деп, С демеушісінің белгілі бір мәніне сәйкес жалпы шешімнен бөлініп алынған шешімді айтамыз. Ендеше, дербес шешім Коши есебінің шешімі болып табылады.

Теорема (Коши есебі шешімінің бар және оның жалғыздығы жөнінде). Егер функциясы D облысында анықталған, үзіліссіз және оның дербес туындысы болса, онда нүктесінің - маңайы, яғни табылып, осы маңайда (9.4) дифференциалдық теңдеудің бастапқы шартты қанағаттандыратын шешімі бар және ол жалғыз болады.

Мысалы, .

Шешуі. Берілген теңдеу бірінші ретті дифференциалдық теңдеу. және анықталған және Оху жазықтығында үзіліссіз. функциясы, мұнда С – ерікті тұрақты, Оху жазықтығындағы берілген теңдеудің жалпы шешімін береді.

(9.4) бірінші ретті дифференциалдық теңдеудің әрбір нүктесіндегі шешімнің жалғыздығы бұзылатын, яғни нүктесі арқылы басқа да (9.4) теңдеуінің шешімдері басып өтетін болса, онда ол ерекше шешім деп аталады.

(9.4) бірінші ретті дифференциалдық теңдеу шешімдерінің геометриялық мағынасы. бірінші ретті дифференциалдық теңдеуі берілсін, мұндағы функциясы облысында анықталған болсын. Бұл теңдеу оған сәйкес шешімнің немесе интегралдық қисықтың бойында жатқан әрбір нүктеге жүргізілген жанаманың бұрыштық коэффициентін береді:

.

облысының кез-келген нүктесінде Ох өсінің оң бағытымен бұрышын жасайтын бірлік (ұзындығы бірге тең) векторлар тұрғызайық. Әдетте вектордың Ох өсімен жасайтын бұрышы деп, осы Ох өсін сағат тілі жүрісінің бағытына қарсы бағытта вектормен беттескенге дейін бұруға қажетті бұрышты айтады. Сонда облысында жататын әрбір нүктесі үшін жанамалар бағыты, осы облыстағы өріс бағыты деп аталады, ал оның интегралдық қисықтары облысында жүргізуге болатын басқа қисықтардан мына қасиетімен ажыратылады: оның кез-келген нүктесінен жүргізілген жанаманың бағыты сол нүктедегі өріс бағытымен беттеседі. Демек, геометриялық тұрғыдан қарағанда, дифференциалдық теңдеуді интегралдау дегеніміз кез-келген нүктесіне жүргізілген жанамасының бағыты осы нүктедегі өріс бағытымен беттесетін қисықты табу болып саналады. Дифференциалдық теңдеудің шешімін өріс бағытын пайдаланып, графикалық жолмен жуықтап салуға болады. Ол үшін изоклиндар әдісі қолданылады. Изоклина деп барлық нүктесінде өрістің бағыты бірдей болатын сызықты атайды. Изоклинаны қиып өтетін барлық интегралдық қисықтар изоклинаның бойында бірдей иіледі, яғни қиылысу нүктесінде осы интегралдық қисықтарға жүргізілген жанамалар 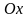өсінің оң бағытымен өзара тең бұрыштар жасайды. «Изоклина» - «біркелкі иілу сызығы» деген аттың өзі де осыдан шыққан. Изоклинаның анықтамасынан оның теңдеуін құру үшін (9.4) теңдеудің оң жағын қандай да болмасын бір тұрақтыға теңестіру керек екендігі шығады. Алынған теңдеу бір параметрлі изоклиналар тобының теңдеуін береді. Параметр - ға әртүрлі ( функциясының түріне байланысты өз қалауымызша) мәндер беру арқылы әртүрлі изоклиналар аламыз.