Расширенное λ-исчисление
λ (λ-абстракция);
@ (аппликация);
TRUE; FALSE; 0,1…; +; /; =; >; <; cons; head; tail (конструкторы данных);
null (распознает пустой список);
If … then… else…;
let;
letrec (позволяет явно записать подстановку); quote (возможно определение через K).
(λx.x+3)3 let x=3 in x+3
letrec fun =H(fun ) in fun(arg)
Пример. a) let x=3 in λy.+xy→ λy.+3y
b) Lisp # '(lambda(x) ML -fun foo [ ]=4 cоns
(cоnd: foo x=(x::3)
(x(cons x’3)) >val foo fn:(’а list)
(# T ’ 4))) →int list
JScript
function foo(x) {
if (x==null) // если список пуст,
then new Array[x,3] //то результат- пара х,3
else 4 // ,иначе 4
}
Расширенное λ - исчисление.
(λх(if x(@
( @ cons x).
(quote 3))
(quote 4))
cons ab →(a,b)
head (cons ab) →a
tail (cons ab) →b
Редукция графа
Любая программа может быть представлена ее синтаксическим деревом разбора.
Так как в “чистом” λ-исчислении всего две операции: λ и @, то будем в дальнейшем их использовать.
Пример. (λх.+х3)4
1-ый способ 2-ой способ
Здесь меняем все свободные вхождения х на 4
В качестве примера свернем это дерево разбора
Определение:
Аппликативный порядок редукции - такой порядок редукции, который предписывает свертывать самый левый из самых внутренних редексов.
Определение:
Нормальный порядок редукции - порядок редукции, который предписывает
свертывать самый левый из самых внешних редексов.
Пример. А: λх. If x≠ 0 then x else 3/Ø . Вычислим А от 4
(Это откровенная ошибка)
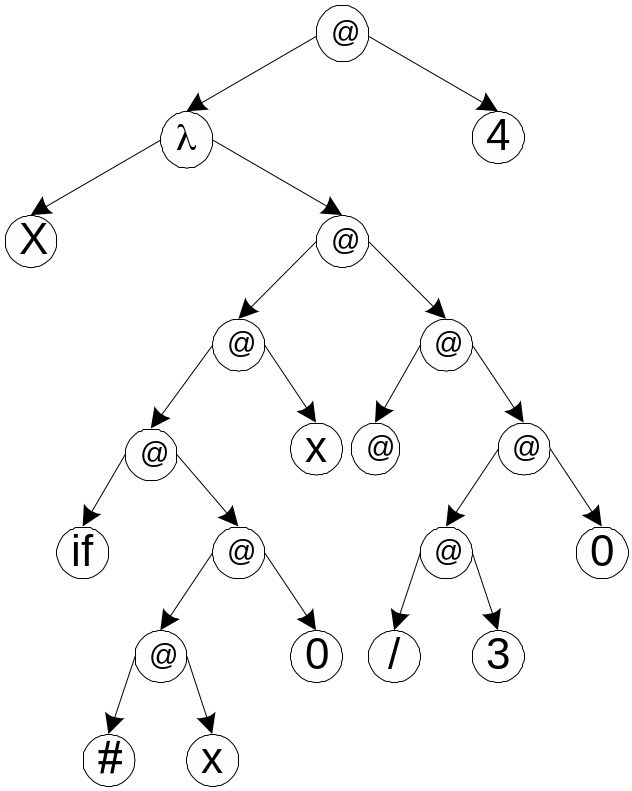
При аппликативном порядке редукции мы
получим ошибку.
При аппликативном порядке вычисляются
все аргументы функции, а уже затем – сама функция.
При нормальном порядке редукции аргументы
вычисляются по мере надобности.
При редуцировании графа мы будем пользоваться
нормальным порядком редукции.
Алгоритм редукции графа (рг)
Редукция графа будет осуществляться циклически.
Повторить:
Спускаемся по левой ветви графа до первой вершины, которая не является аппликацией, т.е. не помечена символом @.
Если эта вершина является корнем графа, то все выражение, находится в нормальной форме, значит окончание вычислений. Если она не является корнем, то она должна являться примитивной функцией либо аппликацией и у нее должны быть все необходимые аргументы (в противном случае ошибка). Мы рекурсивно применяем алгоритм для всех поддеревьев, являющихся аргументами.
Если текущая вершина является λ- вершиной, то рассматриваем следующие варианты:
1. она является корнем графа, значит выражение в нормальной форме.
2. если она не является корнем, то над ней может быть только аппликация @ и мы на место формального параметра λ-абстракции подставляем второе выражение из правой ветви аппликации. При необходимости это поддерево копируется.
Пример. (λх.+хх)7
(λху.+ху)3((λх.х)4)
