Погружение классических вычислений в λ-исчисление.

Определение:

Нумералы- объекты, обладающие свойствами натуральных чисел.

n= λxy.(xⁿ)y n=(SB)ⁿ(KI), здесь S,B,K,I - простейшие комбинаторы

Системы комбинаторов предназначены для выполнения тех же функций, что и системы

- - конверсии

B: Bfgx = f(gx)- элементарный композитор

S: Sfgx = fx(gx) –элементарный коннектор

K: Kcx =c – элементарный канцелятор

I: Ix = x – комбинатор тождества

Пусть z₀= λyx.x (считаем это число нулем). Остальные целые числа введем по индукции: z_n+1=σz_n, где σ - функция добавления единицы: σ = λxyz.y(xyz)

Операция сложения PLUS:

PLUS = λxy.xσy

Утверждается, что PLUSz₀b=b и PLUS(σa)b=σ(PLUSab) (проверяется подстановкой).

Определение:

Усеченная разность: DIF=λxу.yπx, где π-функция предшествования

π=λx.хω(kz₀)z₁, где ω= λx.D(σ(xz₀))(xz₀) πz_i+1=z_i, i ≥ 0

k= λxy.x πz₀=z₀.

D - декартово замкнутое произведение.

D: PROD = λxy.x(yσ)z₀

TRUE λxy.x (так обозначим)

FALSE λxy.y

If X then Y else Z XYZ.

Нумералы.

Введем по индукции обозначение

aⁿb n N nab= aⁿb

a⁰b=b

aⁿ⁺¹b=a(aⁿb)

Пример. a³b=a(a(ab))

Определение:

Нумералом n будем называть λ-выражение вида λху.хⁿy, где n=0,1,2,…

n = λху.хⁿy

n =(SB) ⁿ(KI) (то же выражение, но в терминах комбинаторной логики)

Введем функцию прибавления единицы σ.

σ = λхуz.y(хyz) (σ = λхуz.xy(yz))

σn = n+1

Пример. 0 = λху.y 2 = λху.x(xy)

Покажем, что для таких нумералов (n) σ прибавляет единицу:

┌───────_↓

σnab = (λхуz.y(xyz))( λху.хⁿy)ab = ((( λx.( λy.( λz.y(xyz))))( λx.λy.хⁿy))a)b └───_σ──┘└──_n─┘ ^↑───────────└─────┘

┌────_↓───────_↓ ┌─────────_↓

= ((λy.( λz.(y((λx.λy.хⁿy)yz)))a)b = (λz.a((λx.λy.хⁿy))az))b = a((λx.λy.хⁿy)ab) =

^↑──────────────┘ ^↑──────────┘ └─_n───┘

= a(aⁿb) =aⁿ⁺¹b = /(λху.хⁿ⁺¹y)ab/ = (n+1)ab.

 ↓

σ (SB) ⁿ(KI) = (λхуz.y(xyz))((SB) ⁿ(KI))(λхуz.y(xyz))[(SB) ⁿ(KI)]ab =

^↑──────└─────┘

= a(((SB) ⁿ(KI)a)b) =^B Ba[(SB) ⁿ(KI)a]b =^S SB[(SB) ⁿ(KI)]ab = (SB) ⁿ⁺¹(KI)ab

└_a┘└──_b───┘_{c x z}└──_y──┘ _z

σ^| = λхуz.xy(yz)- альтернативное определение σ, которое также приводится в литературе. Для него можно провести аналогичные выводы.

TRUE λху.x

FALSE λху.y

If x then y else z xyz

Как это проверить?

If TRUE then A else B A

If FALSE then A else B B

┌─_↓

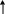( λху.x)AB = A

┌─_↓

( λху.y)AB = B

X&Y If X then Y else FALSE

XVY If X then TRUE else Y

Рекурсия

Определение:

Рекурсивное определение- это определение, которое внутри себя содержит ссылку

на определяемый объект.

Пример. 1) Факториал ƒac(x): x*ƒac(x-1),

if (х=0) then 1 ƒac(0)=1.

else x* ƒac(x-1)

2) Список:

Голова

c ons(x.y)→(x.y) (точечная пара)

head(x.y) →x (голова)

t

nil

ail(x.y) → y (хвост)

length(x)

tail(x) = Nil

length(x) = 1+ length(tail(x))

length(x): if x = Nil then 0

else 1+(length(tail(x))).