4.4.2. Группа конических проекций

Проекции, принадлежащие к группе конических, являются наиболее общими. Теоретически можно показать, что проекции азимутальной и цилиндрической групп представляют собой крайние, предельные случаи группы конических проекций. Пространство у полюсов отображается с разрывами. Во всех классах первого подмножества параллели на плоскости представляют собой дуги окружностей.

Конические проекции. Название обусловлено тем, что при проектировании земной поверхности на плоскость в качестве промежуточной использована поверхность конуса. В данной проекции параллели нормальной сетки – дуги концентрических окружностей, а меридианы – их радиусы, углы между которыми пропорциональны соответствующим разностям долгот.

В нормальной конической проекции воображаемый конус касается Земного шара или сечет его в районе средних широт, поэтому в такой проекции удобнее всего картографировать вытянутые с запада на восток в средних широтах территории России, Канады, США (рис. 4.4.3).

Рис. 4.4.4. Коническая проекция [4]

Псевдоконические проекции. В определенной мере псевдоконические проекции обобщают конические проекции, заменяя в них прямолинейные меридианы криволинейными.

Псевдоконическая картографическая проекция – проекция, в которой параллели нормальной сетки–дуги концентрических окружностей, осевой меридиан – прямая, на которой расположен центр параллелей, остальные меридианы – кривые. Наиболее применимы эти проекции для мировых карт и Тихого океана (рис. 4.4.5).

Рис. 4.4.5. Псевдоазимутальная проекция [4]

Поликонические проекции. Класс поликонических проекций обобщает все подмножество проекций с параллелями постоянной кривизны. Поликоническая картографическая проекция – проекция, в которой параллели нормальной сетки – дуги эксцентрических окружностей, осевой меридиан – прямая, на которой расположены центры параллелей, остальные меридианы – кривые линии.

Наиболее употребительны эти проекции для карт мира (рис. 4.4.6).

Поликонические проекции с параллелями переменной кривизны. В этих проекциях параллели обычно изображаются эллипсами, реже – другими плоскими кривыми. Меридианы – прямые или кривые линии. Известны предложения подобных проекций для карт России, карт Мирового океана и др.

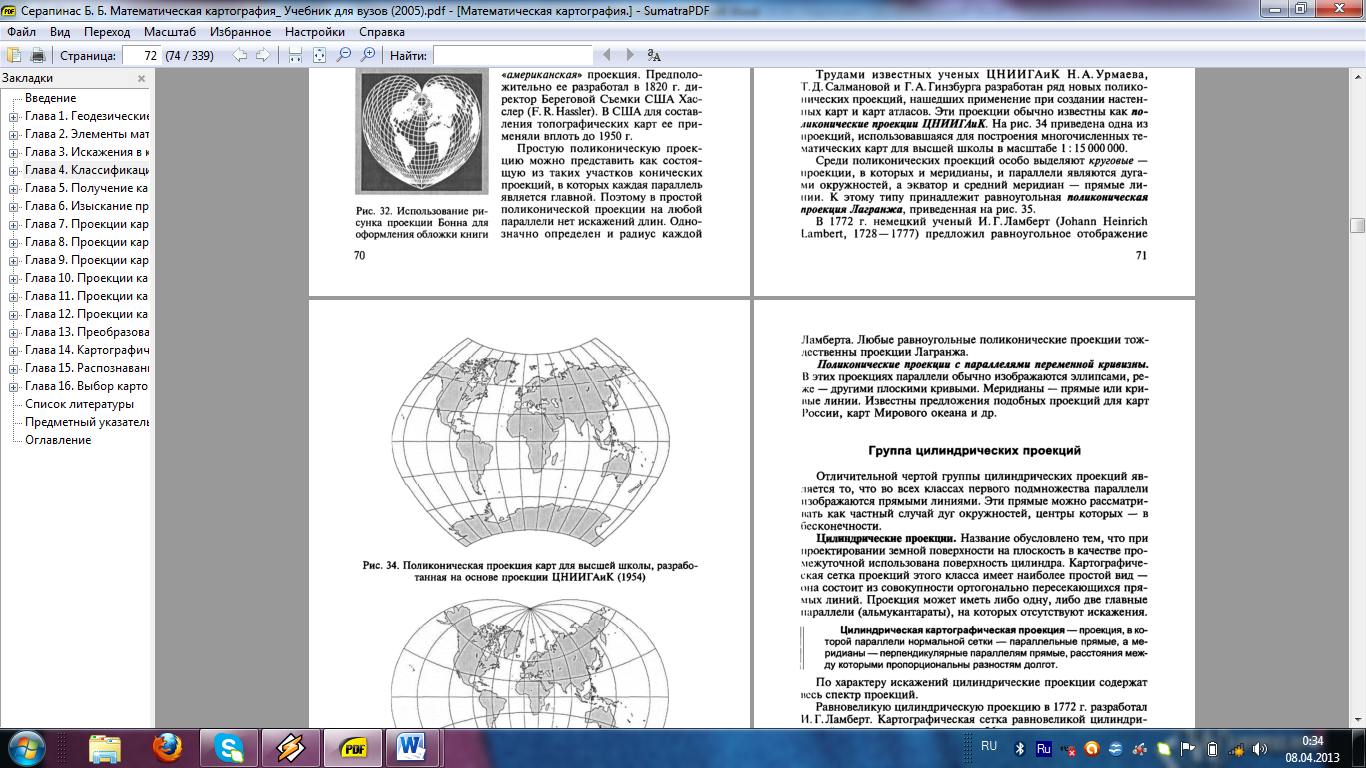
Рис. 4.4.6. Поликоническая проекция [4]

4.4.3. Группа цилиндрических проекций

Отличительной чертой группы цилиндрических проекций является то, что во всех классах первого подмножества параллели изображаются прямыми линиями. Эти прямые можно рассматривать как частный случай дуг окружностей, центры которых – в бесконечности.

Цилиндрические проекции. Название обусловлено тем, что при проектировании земной поверхности на плоскость в качестве промежуточной использована поверхность цилиндра. Картографическая сетка проекций этого класса имеет наиболее простой вид – она состоит из совокупности ортогонально пересекающихся прямых линий. Проекция может иметь либо одну, либо две главные параллели (альмукантараты), на которых отсутствуют искажения. В данной проекции параллели нормальной сетки – параллельные прямые, а меридианы – перпендикулярные параллелям прямые, расстояния между которыми пропорциональны разностям долгот (рис. 4.4.7).

В основном применяются для карт мира и экваториальных государств.

Рис. 4.4.7. Цилиндрическая проекция [4]

Псевдоцилицдрические проекции. Это весьма обширный класс проекций. Вероятно, появление псевдоцилиндрических проекций продиктовано естественным желанием сохранить простой рисунок цилиндрических проекций и устранить их основной недостаток. В цилиндрических проекциях точки полюсов изображаются отрезками такой же длины, как и экватор в этой проекции. Промежутки между меридианами на всех широтах одни и те же. В силу этого на картах возникают значительные деформации изображений полярных районов. В псевдоцилиндрических проекциях полюса могут быть показаны как точками, так и отрезками заданной длины. В данной проекции параллели нормальной сетки – параллельные прямые, средний меридиан – прямая, перпендикулярная параллелям, а остальные меридианы – ломаные прямые или кривые.

Сетка меридианов и параллелей не ортогональна. Поэтому по характеру искажений псевдоцилиндрические проекции бывают либо равновеликими, либо произвольными. Равноугольные проекции в силу геометрической структуры картографической сетки невозможны. Меридианы изображаются ломаными прямыми, а также дугами эллипсов, парабол, гипербол или синусоид.

Нормальные псевдоцилиндрические проекции имеют две оси симметрии –экватор и средний меридиан.

Промежутки между меридианами в равновеликих проекциях пропорциональны разности долгот. В произвольных по характеру искажений проекциях они могут убывать или, значительно реже, возрастать от среднего меридиана к востоку и западу.

Применяются в основном для карт мира, океанов, Африки.

Псевдоцилиндрические проекции в основном применяются для отображения в мелком масштабе крупных частей шарообразной планеты или всей ее поверхности. Поэтому в псевдоцилиндрических проекциях земная поверхность принимается за поверхность шара (рис. 4.4.8).

Рис. 4.4.8. Псевдоцилиндрическая проекция [4]

Как уже отмечалось, псевдоцилиндрические проекции можно рассматривать как частный случай псевдоконических проекций, когда их параллели в пределе из дуг окружностей превращаются в отрезки параллельных прямых линий. Аналогично из поликомических проекций выпрямлением их параллелей получим полицилиндрические проекции. Однако картографические сетки этих двух классов проекций в подмножестве, в котором параллели имеют постоянную кривизну, не будут различаться. Это обусловлено тем, что центры параллелей как псевдоцилиндрических, так и полицилиндрических проекций находятся в бесконечности. Поэтому, хотя в зарубежной специальной литературе встречаются описания полицилиндрических проекций, в российской практике полицилиндрические проекции в отдельный класс не выделяют. Все проекции этого типа классифицируются как псевдоцилиндрические.

Полицилиндрические проекции с параллелями переменной кривизны. В этих проекциях параллели изображаются эллипсами или другими кривыми; меридианы – прямыми или кривыми линиями.

В настоящее время при изыскании картографических проекций не пользуются вспомогательными поверхностями, а строят проекции аналитически. Названия же проекций с применением терминов вспомогательной поверхности позволяет понять их геометрическую суть. При помощи компьютера можно рассчитать любую проекцию с заданными параметрами, а автоматические графопостроители вычертят географическую сетку. Имеются специальные атласы проекций, в том числе и электронные, позволяющие подобрать нужную проекцию для любой территории