Глава 3. Искажения в картографических проекциях
Земная поверхность, имеющая форму сфероида, не может быть развернута в плоскость без деформаций: в одних местах возникают разрывы, для устранения которых необходимо равномерное растяжение, в других – перекрытия, требующие равномерного сжатия. Отсюда следует, что на всех географических картах всегда имеются линейные искажения, и масштаб является величиной переменной, меняющейся с изменением места и направления.
Искажение длин линий (расстояний) связано с изменениями масштаба длин на одной и той же карте и выражается в том, что расстояния одинаковые на эллипсоиде, изображены на карте отрезками разной длины. Различают два вида масштаба длин: главный масштаб, который подписывается на карте, представляющий степень уменьшения поверхности земного эллипсоида перед последующим изображением его на плоскости и сохраняющийся в зависимости от применяемой картографической проекции в некоторых точках или линиях, называемых точками и линиями нулевых искажений и частный масштаб, представляющий отношение бесконечно малого отрезка в данной точке и по данному направлению к соответствующему бесконечно малому отрезку на эллипсоиде. В бесконечно малой окрестности каждой точки карты различают:
m – частный масштаб длин по меридиану;
n – частный масштаб длин по параллели;
θ– угол между меридианом и параллелью
Отношение частного масштаба к главному характеризует искажения длин μ в данной точке и рассчитывается по формуле:
μ=
Два взаимно перпендикулярных направления в каждой точке карты, по которым частные масштабы длин имеют наибольшее и наименьшее значения (экстремальные масштабы) называются – главными направлениями в картографической проекции. Обычно экстремальные масштабы обозначаются буквами:
a – наибольший масштаб;
b – наименьший масштаб.
Проекции в которых угол θ=90, называются ортогональными. Из этого следует отношение a=m, b=n или a=n, b=m [4].
Для неортогональных проекций, используя значения частных масштабов по меридиану и по параллели m и n, а также угол между меридианом и параллелью θ, экстремальные масштабы длин a, b и азимут β главного направления на карте вычисляют по формулам:
[4]
Наличие искажений длин линий ведет к искажению углов, площадей и форм бесконечно малых фигур. Искажения на картах могут быть определены посредством: измерений по карте с последующими вычислениями, макетов карт с изоколами, номограмм и таблиц.
Искажение углов заключается в том, что, углы между направлениями на карте не равны соответствующим углам на эллипсоиде. Величина искажения угла в данной точке карты зависит от направления сторон угла. В качестве показателя искажения углов на карте принято наибольшее искажение ω. В любой точке карты всегда имеется угол, изображающийся без искажения и равный 90º, который соответствует главным направлениям эллипса (осям) искажений. Для характеристики искажения углов на карте между меридианами и параллелями, которые на поверхности эллипсоида встречаются под прямым углом, используют его отклонения от 90º и обозначают греческой буквой ε (эпсилон), т.е. ε=θ-90º.
Разные углы, имеющие вершину в заданной точке, искажаются по-разному. Так, углы между главными направлениями не искажаются вовсе. Поэтому оцениваются максимальные искажения (ω). Существует ряд формул для их вычисления. Одна из основных:
[4]
Искажение углов и длин линий на карте вызывает искажение форм контуров бесконечно малых размеров, который оцениваются коэффициентом форм:
[4]
С искажением длин также связанно и искажения площадей, вследствие различия масштаба площадей в разных точках карты. Для оценки искажения площадей используют такое понятие, как частный масштаб площадей. Частный масштаб площади может быть определен по одной из следующих формул
=
ab [4]
Существуют разные наглядные способы отображения искажений, такие как: профили головы человека, изоколы, эллипсы искажений и др.
Изаколы – линии соединяющие точки с одинаковыми количественными значениями определенного показателя. Изоколы строятся для любых показателей искажений: длин, площадей, углов, форм. Изоколы характеризуют искажения отдельных видов. Они получили распространение благодаря простоте построения.
На рис. 3.1 для примера приведен макет карты с изоколами частного масштаба площадей р и наибольшего искажения углов ω.
Рис. 3.1. Изоколы частного масштаба площадей (слева) и наибольшего искажения углов (справа) [4]
Эллипс искажений в данной точке карты изображает бесконечно малый круг на поверхности эллипсоида или шара. Полуоси эллипса равны экстремальным масштабам длин a и b, они ориентированы по главным направлениям. Его размеры и форма характеризуют все виды искажений на карте – длин, площадей, углов и форм (рис. 3.2).
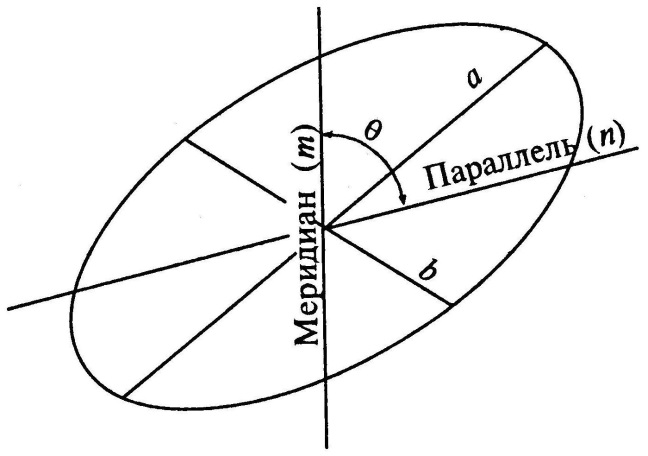
Рис. 3.2. Эллипс искажений и его элементы [9]
Недостатком изокол и эллипсов искажений является то, что по ним трудно судить об искажениях на картах крупных объектов конечных размеров, например, таких, как материки и океаны.