Основные понятия и законы гидростатики

В гидростатике рассматривается равновесие жидкостей, находящихся в общем случае, в состоянии относительного покоя, при котором в движущейся жидкости ее границы не перемещаются друг относительно друга. При этом силы внутреннего трения отсутствуют и жидкость можно рассматривать как идеальную.

Пример: движущаяся цистерна с жидкостью.

В неподвижном сосуде жидкость находится в абсолютном покое, который является частным случаем относительного покоя.

Представим себе элементарную площадку внутри объема покоящейся жидкости. Независимо от положения площадки в данной точке объема на нее будет действовать сила давления жидкости, направленная по нормали к элементарной площадке. Силу, отнесенную к единице площади, называют средним гидростатическим давлением:

Предел называется давлением в данной точке. сила давления.

Размерность давления:

Свойства гидростатического давления:

1. Гидростатическое давление всегда направлено по нормали к поверхности, с которой жидкость соприкасается.

Если бы сила давления была направлена под углом, то ее можно было бы разложить на нормальную и касательную составляющие. Последняя бы вызвала перемещение жидкости, что противоречит условию ее не подвижности.

2. Величина гидростатического давления в любой точке одинакова по

всем направлениям, иначе также происходило бы перемещение жидкости.

В различных же точках давление различно, в зависимости от положения этих точек в жидкости.

Дифференциальное уравнение равновесия Эйлера

Задача – выяснить закон распределения гидростатического давления по объему жидкости (интегр.)

В объеме капельной жидкости, находящейся в абсолютном покое, выделим элементарный параллелепипед объемом с ребрами , расположенными параллельно осям координат

Сила тяжести, действующая на параллелепипед, выражается произведением его массы

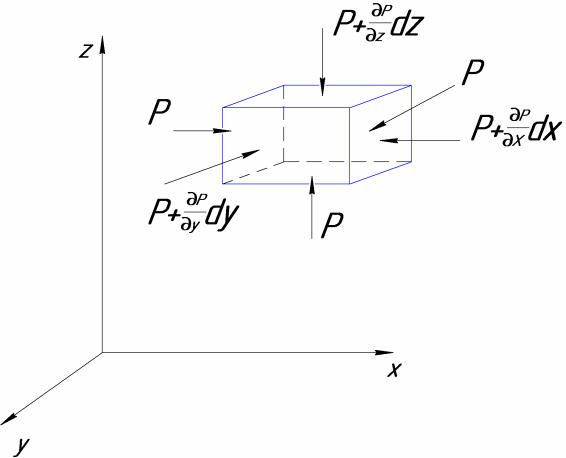
Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю.

В противном случае происходило бы перемещение жидкости.

Сумма проекций сил на ось z:

1. Сила тяжести проектируется со знаком

2. Сила гидростатического давления на нижнюю часть:

3. На верхнюю часть давление больше

Сумма проекций на оси

Проекции сил тяжести на эти оси равны нулю.

Ось :

Ось :

Условия равновесия элементарного параллелепипеда выражается системой уравнений:

дифференциальное уравнение равновесия Эйлера

Давление в покоящейся жидкости изменяется только по вертикали, оставаясь одинаковым во всех точках любой горизонтальной плоскости, т.к. изменения давлений вдоль осей равны нулю.

Для получения закона распределения давления во всем объеме покоящейся жидкости, необходимо проинтегрировать систему уравнений.

Основные уравнения гидростатики

Умножим левые и правые части уравнения соответственно на и сложим:

Так как гидростатическое давление меняется только по вертикали, т.е. , то можно заменить частную производную на полную:

Частные производные определяют изменения гидростатического давления в точке в направлении соответствующих осей, а величины

Определяют изменения давления на длине ребер.

Сумма членов в скобках выражает изменение давления во всем рассматриваемом элементарном объеме, поэтому используется полный дифференциал гидростатического давления

Представим это уравнение в виде:

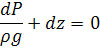
Для несжимаемой однородной жидкости уд. вес = const

Откуда получаем:

Для двух произвольных горизонтальных плоскостей 1 и 2 уравнение выражают в виде:

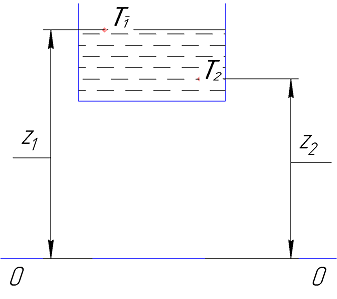
где высоты (нивелирная высота) расположения двух точек внутри покоящейся однородной капельной жидкости над произвольно выбранной горизонтальной плоскостью отсчета (плоскостью сравнения), гидростатические давления в этих точках.

Например, для двух точек:

Для каждой точки покоящейся жидкости сумма нивелирной высоты и статического напора есть величина постоянная.

Имеется определенный энергетический смысл (уд. энергия на ед. веса)

Нивелирная высота (геометрический напор) представляет собой удельную потенциальную энергию положения данной точки над выбранной плоскостью сравнения, а статический напор – удельную потенциальную энергию давления в этой же точке. Сумма этих энергий равна общей потенциальной энергии, приходящейся на единицу веса жидкости.

Следовательно, основное уравнение гидростатики представляет собой частный случай закона сохранения энергии: удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная.

Давление, создаваемое в любой точке покоящейся несжимаемой жидкости, передается одинаково всем точкам ее объема.

При изменении в точке , изменяется во всякой другой точке жидкости.