3.3. Накопленная сумма единицы

При определении "ставки дохода на инвестиции" как основного финан- сового критерия во внимание следует принять эффект сложного процента. Сложный процент означает, что уже полученный процент, будучи положенным на депозит вместе с первоначальными инвестициям становится частью основной суммы. Поэтому в следующий период наряду с первоначальным депозитом он также приносит новый процент. Напротив, простой процент не предполагает получения процента на процент.

Например, предположим, что 100 долл. депонированы на счет, ставка по которому составляет 10% и этот процент накапливается раз в год. В первый год 100 долл. принесут 10 долл. процента (10% от 100 дол = 10 долл.).

В конце первого года остаток составит 110 долл. (100 дол + 10 долл. =110 долл.). Если в течение второго года вся сумма в 110 долл. будет оставаться на депозите, то во второй год процент составит уже 11 долл. (10% от 110 долл. = 11 долл.). По истечении 5 лет остаток составит уже 161,05 долл. при условии, что весь процент остается на депозите. Это показано в табл. 3.1. Для сравнения: при простом проценте ежегодный доход на инвестиции составит 10 долл.; поэтому через

ТАБЛИЦА 3.1

Депозит 100,00 долл. — сложный и простой процент (ставка = 10%)

Год		Сложный	Простой
		процент	процент
0	Депозит	100,00	100,00
1	Полученный процент	10,00	10,00
1	Остаток, конец года	110,00	110,00
2	Полученный процент	11,00	10,00
2	Остаток, конец года	121,00	120,00
3	Полученный процент	12,10	10,00
3	Остаток, конец года	133,10	130,00
4	Полученный процент	13,31	10,00
4	Остаток, конец года	146,41	140,00
5	Полученный процент	14,64	10,00
5	Остаток, конец года	161,05	150,00

5 лет накопленная сумма будет равна 150 долл. (100 долл. + 5 X 10 долл. = 150 долл.), что также видно из табл. 3.1.

Сила сложного процента может быть показана на следующем при­мере. Если бы индейцы, продавшие в 1626 г. остров Манхэттен Питеру Миньюту за товары стоимостью 24 долл., инвестировали эти 24 долл. под ежегодно накапливаемые 6%, то в 1983 г. сумма этих вложений составила бы почти 26 млрд.долл. Если бы индейцы инвестировали под ежегодно накапливаемые 7%, то остаток достиг бы астрономической суммы 741 млрд.долл. Логика сложного процента очевидна. Все деньги, которые оставле­ны на депозите, должны приносить процент. Более того, процент при­носят только те деньги, которые оставлены на депозите. Эту инвестици­онную логику необходимо твердо усвоить всем финансовым аналити­кам и оценщикам.

Рис. 3.1 показывает графически рост основной суммы сегодняш­них вложений до расчетной будущей стоимости с учетом сложного процента.

Предварительно рассчитанные таблицы сложного процента

Поскольку сложный процент применяется очень часто и широко, инве­сторы считают удобным и целесообразным воспользоваться стандарт­ными таблицами, содержащими предварительно рассчитанные факто­ры сложного процента. Фактором (factor) называется одно из двух или более чисел, которые, будучи перемноженными, дают заданный резуль­тат. Если инвестор знает, какова будет стоимость 1 долл. к концу 23-го года при ежегодном накоплении 10%, то он также может узнать, какова будет стоимость 43,22 долл.

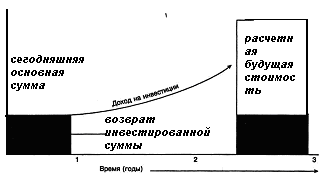
Рис. 3.1. Рост основной суммы по сложному проценту

— умножив 43,22 долл. на стоимость 1 долл. к концу 23-го года., т.е. будущая стоимость денег определяется по формуле:

где: FV- будущая стоимость денег;

PV- текущая стоимость денег;

(1+E)ⁿ – фактор сложного процента.

Во всех таблицах сложного процента исполь­зуется формула:

где:

Sⁿ = сумма после п периодов;

Е = периодическая ставка процента;

п число периодов.

Большинство "шестифакторных" таблиц сложного процента показы­вает рост 1 денежной единицы (доллара, рубля, евро) в колонке 1.

Более частое накопление

Нередко период накопления короче года. Накопление может происхо­дить ежедневно, раз в месяц, в квартал или в полгода. Обычно устанав­ливается номинальная годовая ставка, например 10%, однако при более частом накоплении эффективная ставка процента повышается. Общая формула остается той же:

Sⁿ =(1 + Е)ⁿ,

однако с учетом сокращения периода накопления в нее должны быть внесены изменения.

При корректировке данной формулы число лет, на протяжении ко­торых происходит накопление, умножается на его частоту в течение од­ного года; одновременно номинальная годовая ставка процента делит­ся на частоту накопления. Результат покажет эффективную ставку про­цента за период накопления.

Пример 3.3. Вклад в сумме 1000руб. размещен на 1 год под 10 % годовых. Проценты начисляются ежеквартально. Необходимо опре­делить: периодическую ставку процента, будущую стоимость вкла­да, доход на капитал (Д).

Решение:

1.

2. Доход = 1103,8 - 1000 = 103,8 руб.