Площадь криволинейной трапеции

Найдём 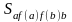– площадь криволинейной трапеции .

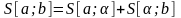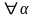Очевидно, для . Для 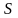выполняется условие (1.3)

.

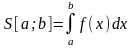Объём тела вращения

Пусть 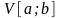– объем тела вращения криволинейной трапеции относительно OX: – АФОП.

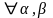
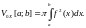
Объём тела вращения относительно OY:

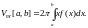
Пример 1.8. Объём шара

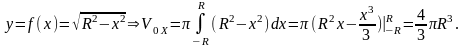
Длина пути

Определение 1.13. Путем в 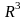называется отображение числового промежутка 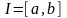в , где

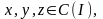
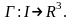
Определение 1.14. 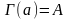– начало пути, 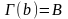– конец пути.

Определение 1.15. Путь называется замкнутым, если .

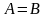Определение 1.16. Путь, для которого отображение взаимно однозначно называется простым путем или параметризованной кривой, а его носитель (образ 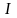) – кривой в .

Определение 1.17. Путь называется путем данного класса гладкости, если 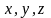принадлежат указанному классу ( ).

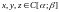Если эти функции класса , то отображение будет гладким, кривая тоже гладкая.

Путь называется кусочно-гладким, если 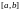можно разбить на конечное число отрезков, на каждом из которых отображение гладкое.

Всюду ниже будем рассматривать кусочно-гладкие пути.

Задача определения длины пути , пройденного за время

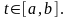
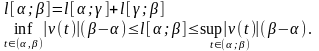
Скорость точки 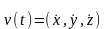, 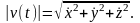В силу Теоремы 1.11

.

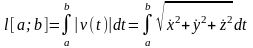Для плоской кривой

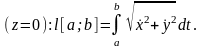
Если кривая задана в декартовых координатах уравнением:

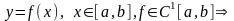
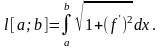
Если кривая задана в полярных координатах уравнением:

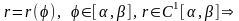
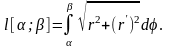
Пример 1.9.

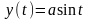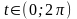, , – окружность

.

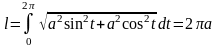Площадь поверхности тела вращения

Площадь поверхности 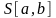тела вращения кривой 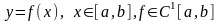вокруг оси

Лекция №7

1.3. Несобственный интеграл

Определение 1.18. Несобственный интеграл первого рода.

Пусть 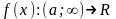, ,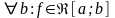 тогда несобственный интеграл 1-го рода. Если существует конечный предел: , говорят, что несобственный интеграл сходится. В противном случае интеграл расходится.

Геометрический смысл сходящегося интеграла: – площадь под графиком функции 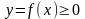конечна.

Пример 1.10.

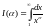– при каком интеграл будет сходиться?

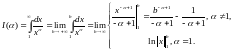
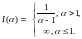
Интеграл сходится при .

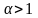Определение 1.19. Несобственный интеграл второго рода.

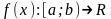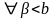
Пусть , 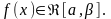Функция не ограничена в окрестности точк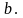и Если – несобственный интеграл от неограниченной функции сходится.

Аналогично, если функция не ограничена в окрестности точки :

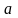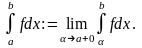
Пример 1.11.

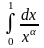– сходится при .

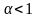Определение 1.20. Пусть функция задана , 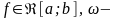особая точка (либо функция не ограничена в ее окрестности, либо )

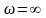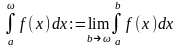несобственный интеграл с особенностью в

Свойства несобственного интеграла

1. Если несобственный интеграл совпадает с определенным.

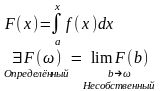
( Из непрерывности ).

2. Линейность интеграла.

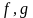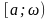Если функции – интегрируемы на в несобственном смысле

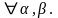
3. Аддитивность по промежутку

Если 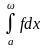– несобственный интеграл сходится

4. Формула замены переменных

Если 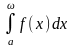– сходится,

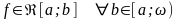
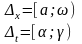
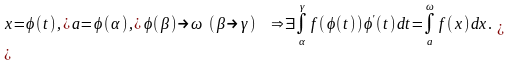
Доказывается с помощью предельного перехода и свойства интеграла Римана.

Если функция 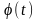гладкая и существует 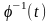, то и 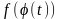сходятся или

расходятся одновременно.

5. Cвойство, связанное с неравенствами

Есл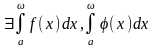и и .

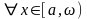
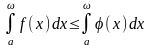6. Интегрирование по частям

Пусть

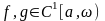
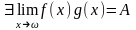
и сходятся или расходятся одновременно и

.

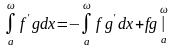Из формулы интегрирования по частям в собственном интеграле.

Критерий Коши сходимости несобственного интеграла

.

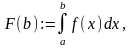
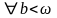Теорема 1.12. Критерий Коши

сходится .

◄ .

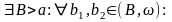
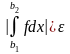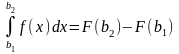В силу критерия Коши для функции .►

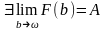Определение 1.21.

Будем говорить, что сходится абсолютно, если сходится интеграл .

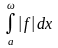Утверждение 1.13. Если интеграл сходится абсолютно он сходится.

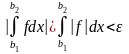◄ .(Следует из критерия Коши и свойств интеграла Римана.) ►

Определение 1.22. Если интеграл сходится, но при этом расходится абсолютно интеграл сходится условно.

Обозначим

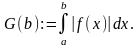
Утверждение 1.14.

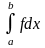сходится абсолютно 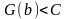(ограничена сверху)

◄ .►
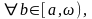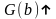
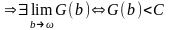