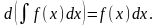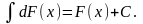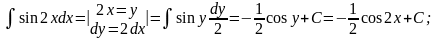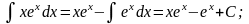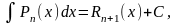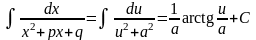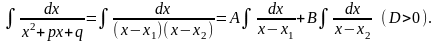Московский Авиационный Институт

(Национальный исследовательский университет)

Иванова Е.П.

Математический анализ

Интегральное исчисление функций одной переменной

Дифференциальное исчисление функций многих переменных

8 факультет

1 курс 2 семестр

(специальность 010501, 230401)

2013 г.

Оглавление

Предисловие

Данное учебное пособие представляет собой конспект лекций второго семестра основного курса математического анализа, читаемого автором на факультете прикладной математики и физики МАИ.

Оно состоит из следующих разделов: интегральное исчисление функций одной переменной и дифференциальное исчисление функций многих переменных.

Обозначения

- пространство действительных чисел;

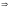- следует;

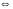- тогда и только тогда;

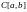- множество функций, непрерывных на ;

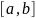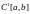- множество функций, непрерывно-дифференцируемых на ;

- множество функций, интегрируемых на ;

Лекция №1 Глава 1. Интегральное исчисление функций одной переменной

1.1. Первообразная. Неопределенный интеграл

Определение 1.1. Пусть задана , .

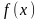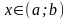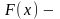первообразная для на некотором промежутке, если

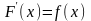
_{на этом промежутке.}

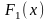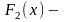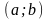Утверждение 1.1. Если и две первообразные для на , тогда .

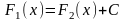◄ Пусть

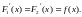
В силу следствия из теоремы Лагранжа: функция равна постоянной тогда и только тогда, когда ее производная равна нулю: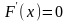

►

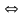
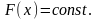
Замечание 1.1. Условие, что и 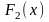сравниваются на связном промежутке, существенно.

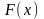
Определение 1.2. Пусть задана , а ее первообразная, тогда неопределенный интеграл, где произвольная постоянная,

подынтегральная функция, 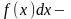подынтегральное выражение.

Свойства интегралов

1. Линейность

Пусть

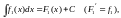
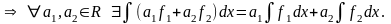
◄ Так как .

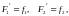
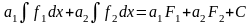В то же время 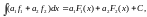поскольку ►

2. 

3. 

◄ ►

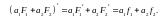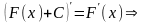
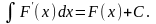4. Формула интегрирования по частям:

◄ ►

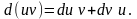
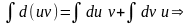
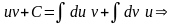5. Замена переменной в интеграле

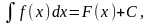
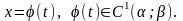
_Тогда

◄ ►

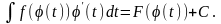
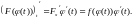Пример 1.1.

• 

• 

• 

• 

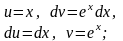
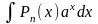• , то

• 

• 

• 

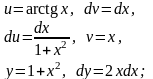
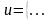
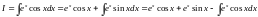
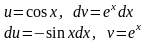
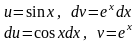
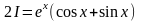
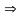
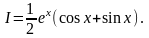
Существуют интегралы, не выражающиеся в элементарных функциях, например:

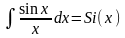• интегральный синус,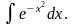

• 

Интегрирование рациональных выражений

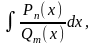
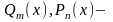многочлены с действительными коэффициентами,

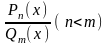правильная дробь.

1. 

2. 

3. 

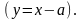
(выделили полный квадрат:

4. 

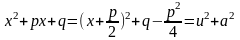
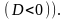
Пример 1.2.

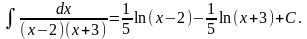
Метод неопределенных коэффициентов:

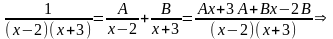
1-ый способ:

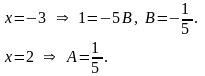Или 2-ой способ:

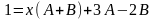
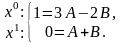
Пример 1.3.

.

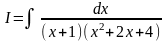
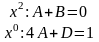
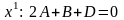
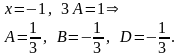
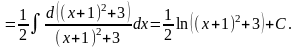
Утверждение 1.1 (основная теорема алгебры). Многочлен 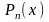с действительными коэффициентами имеет ровно 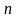, вообще говоря, комплексных корней.

_{Утверждение} 1.2. Если 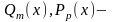многочлены с действительными коэффициентами,

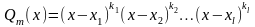
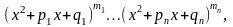
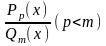правильная дробь.

Тогда существует единственное представление:

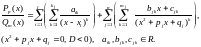
Утверждение 1.3. Интеграл от рационального выражения всегда выражается через рациональные функции, логарифм и арктангенс.

◄ В силу утверждения 1.2 остается рассмотреть случаи:

1. 

2. 

3. 

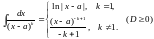
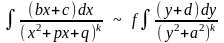
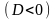
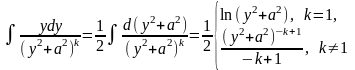
4. Обозначим

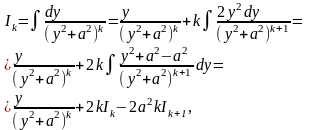
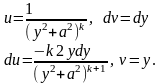
Получаем рекуррентную формулу:

►
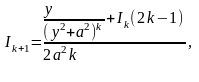
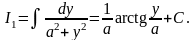