Лекция №17 Неявные функции

Определение 2.41. Функция , заданная в называется неявной функцией, заданной уравнением если :

Теорема о неявной функции

Теорема 2.16 (скалярный вариант теоремы о неявной функции).

,

1. 

2. ,

3. ,

4. .

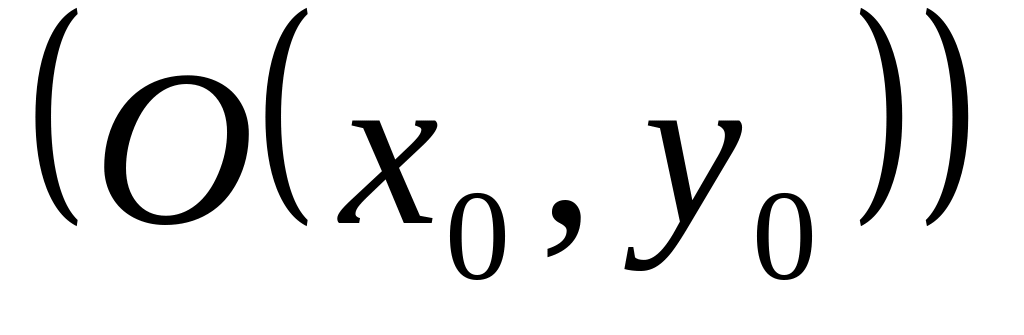
Тогда , , что 1) задаёт неявную функцию т.е. , при этом

1) ,

2) ,

такая – единственна.

◄ 1. Существование.

Пусть для определенности ( ).

Так как – непрерывна, в некоторой окрестности точки пусть это круг радиуса .

Обозначим , ,

, ,

, = , .

,

,

, – строго возрастающая по , непрерывная, принимающая на концах значения разных знаков

, .

Таким образом: ,

– неявная функция, т.к. функция строго возрастает – единственная .

2. Покажем, что :

:

, если .

Если в качестве взять любое получим по определению непрерывность в

3. Покажем, что .

Пусть , , .

По теореме о среднем

+ .

при

(

Так как – непрерывна, то . Так как то при

= .

В силу непрерывности композиции функций непрерывна .

Если

, ,

по индукции .►

Пример 2.18.

,

,

,

,

.

Непосредственно:

, .

Теорема 2.17 (общий вариант теоремы о неявной функции).

1) , , , , ;

2) ;

3) , ;

4)

,

,

1)

;

2) ;

3) .

◄ В доказательстве аналогично скалярному случаю. ►

Пример 2.19.

,

?

, ,

,

Лекция №18 Дифференциал отображения f:

Определение 2.42. Пусть задано отображение , дифференцируемые.

Тогда матрица – называется матрицей Якоби отображения

.

Строки матрицы градиенты функций ,

Пусть Рассмотрим столбцов матрицы с номерами ; – независимых переменных.

Определение 2.43.

– Якобиан отображения f (определитель матрицы Якоби).

Определение 2.44. Отображение называется невырожденным, если хотя бы один из Якобианов отличен от нуля ( или – линейно независимы).

Определение 2.45. Линейное отображение называется дифференциалом отображения , если при .

Тогда отображение называется дифференцируемым, а главная линейная часть называется дифференциалом.

Определение 2.46. Отображение , называется гладким, если – гладкие.

Свойства дифференциала отображения

, , .

1. Если дифференциал существует, то он единственный;

2. ;

3. , , ,

;

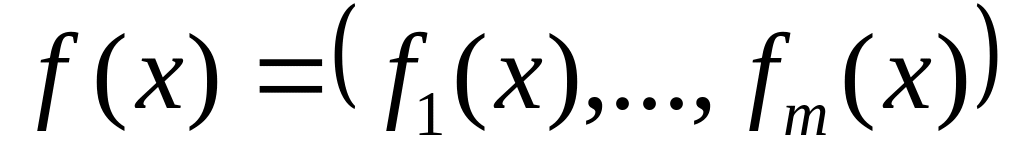4. – дифференцируема в точке а, ;

– дифференцируема в точке , ;

, – дифференцируема в точке а и

◄ По правилу дифференцирования сложной функции

.

По правилу умножения матриц

= ►

5. Если

.

6. , , .

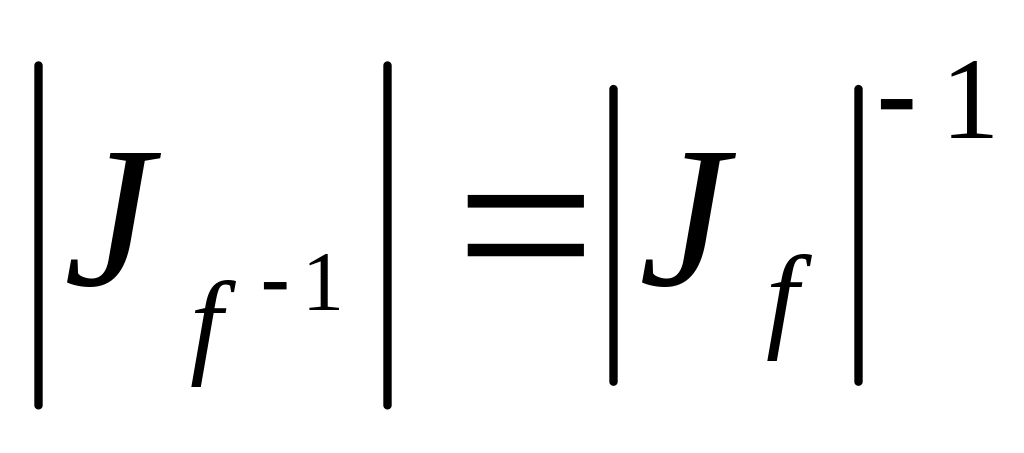◄ Если в О(а), f – биекция, , ,

, .►

Лекция №19 Теорема о системе неявных функций

Введём обозначения: .

Теорема 2.17.

1) , , , ,

, V – область в ;

2) , ;

3) , ;

4)

, :

1)

,

2) ,

3) .

Замечание 2.4. Если линейное отображение, то утверждение теоремы есть факт из линейной алгебры о решении системы линейных уравнений.

Определение 2.47. .

Отображение f называется диффеоморфизмом класса р, если

1. ,

2. f – биекция,

3. 

Теорема 2.18 (об обратном отображении).

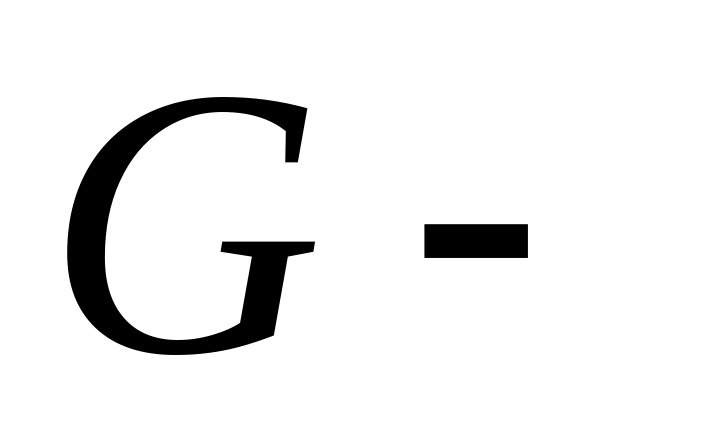1. , открытое.

2. ,

3. 

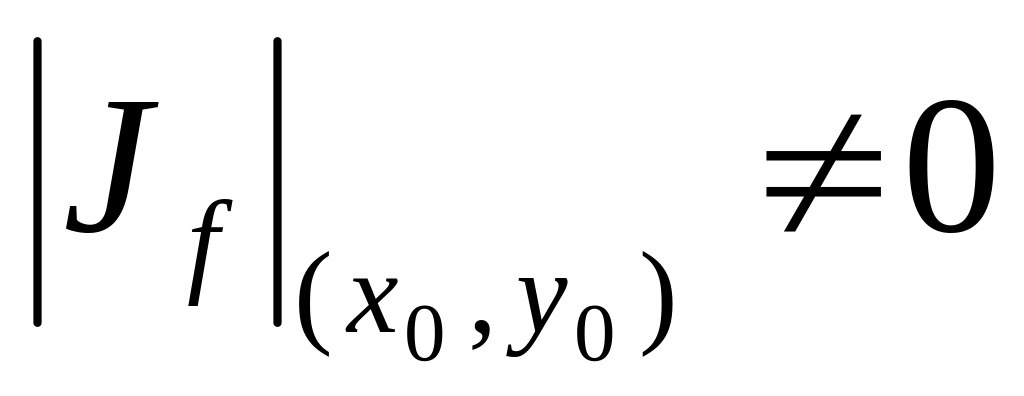
– является диффеоморфизмом.

, .

◄ .

По теореме о системе неявных функций

, ,

Таким образом, отображения взаимно однозначны.

.

Если – внутренняя точка G, то – внутренняя точка , так как

– прообраз отображает открытое в открытое и наоборот (так как условия теоремы выполнены и для функции ). ►

Теорема 2.19 (принцип сохранения области).

1. , G – область (открытое, связное множество),

2. 

– область.

Гладкое отображение с неравным нулю Якобианом отображает область в область.

Доказательство того что образ открытого открытое в теореме 2.18; остается доказать связность.

Пример 2.20.