Касательная плоскость и нормаль к поверхности в r3

Определение 2.33. Поверхностью в назовем график функции

Г= ( Г– график непрерывной функции).

Определение 2.34. Пусть заданы две поверхности: и точки .

Будем говорить, что две поверхности имеют касание первого порядка в точке , если

Теорема 2.10. Пусть функция дифференцируема в окрестности точки , , тогда плоскость

является касательной плоскостью к поверхности в точке .

◄ Так как функция дифференцируема, то

– это означает, что поверхности касаются друг друга. ►

Геометрический смысл дифференциала: приращение аппликаты касательной плоскости.

Определение 2.35. Нормаль к поверхности – это вектор с координатами .

Пример 2.14. Написать уравнение касательной плоскости и нормали к поверхности

в точке

, , , .

;

– уравнение касательной плоскости,

– вектор нормали,

– уравнение нормали.

Определение 2.36. область, если это открытое и связное множество.

Теорема 2.11 (о среднем).

дифференцируема на

◄ Введем функцию одной переменной:

,

Используем формулу Лагранжа: ►

Следствие 2.3. G – область, , f – дифференцируемая функция; .

◄ если .

Пусть . 1. Докажем, что где B – шар в :

и

функция константа.

2.Докажем для G. Так как G связно, : , Г( )=b, Так как G открыто, все точки кривой содержатся в G вместе с некоторыми шарами. Из точки можно переместиться в точку , оставаясь внутри этих шаров. В силу пункта 1. в каждом шаре функция постоянна, следовательно ►

Лекция №15 Частные производные высших порядков

Пусть ;

– частная производная второго порядка.

По индукции можно ввести частные производные высших порядков.

Частная производная n-го порядка – это частная производная от производной порядка .

Если , то производные смешанные.

Пример 2.15. ,

, ,

.

Теорема 2.12 (Шварца о независимости смешанных производных от порядка дифференцирования).

Пусть и в О(a) и в самой точке а эти производные непрерывны .

◄ Докажем для n=2: , ,

обозначим

Введем функции:

тогда

= (по формуле Лагранжа)

=

(в силу непрерывности второй производной в точке a) = .

Аналогично .

Осуществив предельный переход, получим равенство вторых производных. ►

Следствие 2.4. Если частные производные до n-ого порядка существуют и непрерывны в точке а, то они не зависят от порядка дифференцирования.

Следствие 2.5. В пространстве (пространство функций, имеющих непрерывные частные производные до k-ого порядка включительно) производные не зависят от порядка дифференцирования.

Определение 2.37. Функция называется n раз дифференцируемой, если все производные (n -1)-го порядка дифференцируемы.

Утверждение 2.17 (достаточное условие дифференцируемости до n-го порядка). Функция будет n раз дифференцируемой, если она принадлежит пространству .

Дифференциалы высших порядков

Пусть

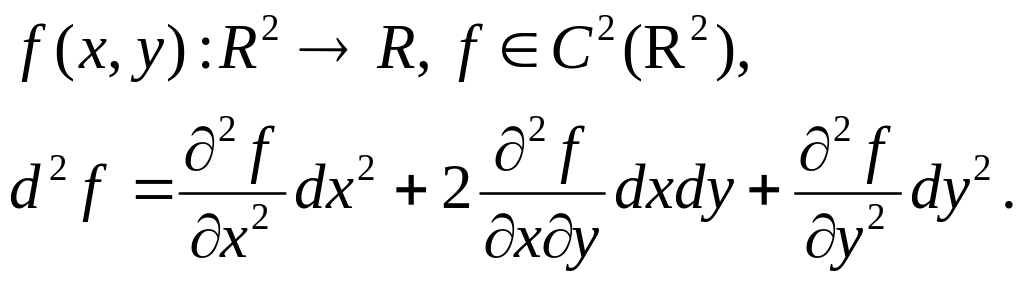
Нарушение инвариантности формы дифференциалов высшего порядка

Для дифференциала первого порядка инвариантность формы сохраняется:

Для дифференциалов высшего порядка инвариантность нарушается

1. Если x – независимая переменная, то ,

2. если , то .

Замечание 2.2. Если – линейное преобразование, то инвариантность формы второго дифференциала сохраняется: