Конкретизация баз

1. База в :

, элементы базы – проколотые окрестности

: ;

: 0< ;

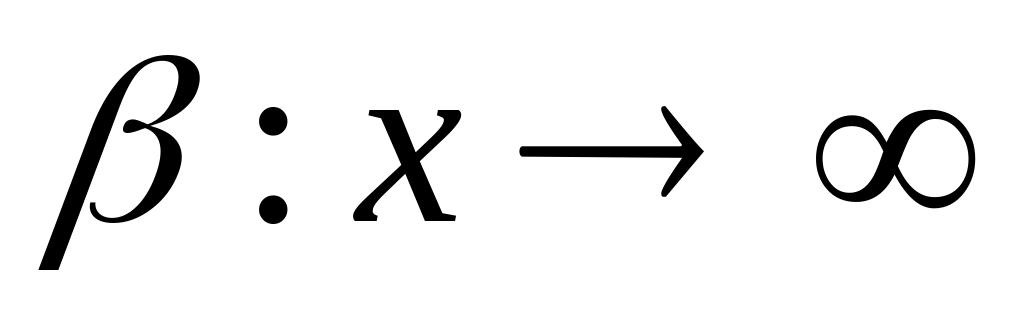2. База в :

: ;

элементы базы-- окрестности бесконечно удаленной точки:

: .

Пример 2.9. Пусть

База элементы базы: .

элементы базы , при этом

В силу теоремы о пределе композиции

Пример 2.10.

не существует, т.к. если , то , если , то .

Определение 2.20. Пределы , называются повторными пределами.

Замечание 2.1. Из существования повторных пределов не следует существование предела функции. В этом можно убедиться на примере.

Пример 2.11.

Повторные пределы существуют и различны. При этом не существует.

Лекция № 12 Непрерывность отображения f :

Пусть , точка – предельная для E.

Определение 2.21. – непрерывна в точке , если

1.

2.

3. .

Локальные свойства непрерывных отображений

1. Если 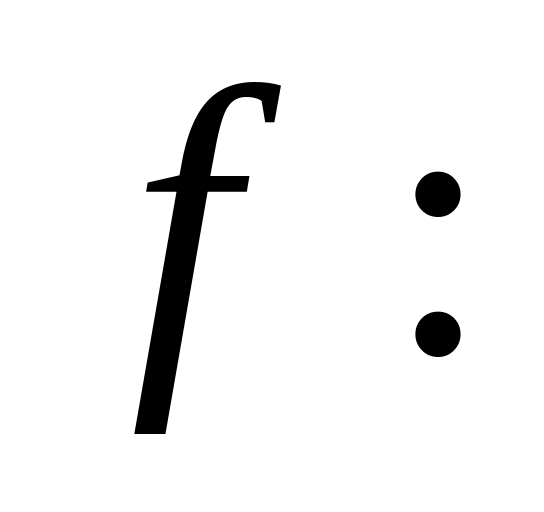непрерывна в точке , то она финально ограничена при

(ограничена в некоторой окрестности );

2) арифметические свойства

– непрерывны в точке а

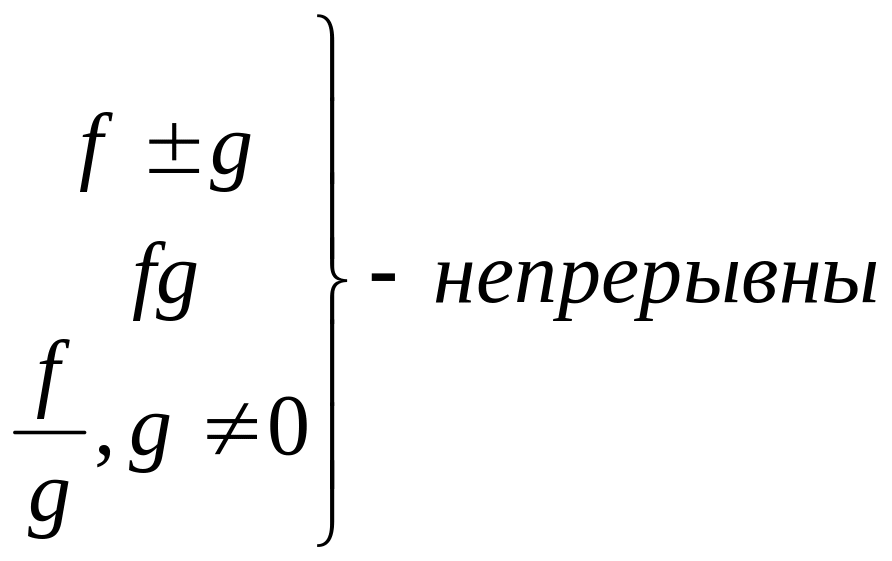в точке

3) , – непрерывная в точке а и ;

4) ,

,

f – непрерывна в точке непрерывна в точке - непрерывна в точке

Свойства 1-4 основаны на свойствах предела.

Пример 2.12.

Не существует : при , при .

В точке (0,0) функция разрывна.

При фиксированном , при фиксированном функция непрерывна в нуле по обеим переменным.

Замечание 2.2. Если функция непрерывна по каждой из своих переменных, из этого не следует непрерывность функции по совокупности переменных.

Глобальные свойства непрерывных отображений Равномерная непрерывность

.

Определение 2.22. f – непрерывна на , если она непрерывна в каждой точке этого множества. Обозначение:

Определение 2.23. f – равномерно непрерывна на , если .

Утверждение 2.12. равномерно непрерывна на она непрерывна на .

Теорема 2.5 (Кантора). непрерывна на компакте она равномерно непрерывна на нем.

◄ непрерывна на : , где .

Построим покрытие компакта системой открытых множеств:

. Выделим из этой системы конечное подпокрытие: (по определению компакта). Обозначим

Покажем:

Для . Покажем, что :

, .►

Теорема 2.6 (Вейерштрасса). Если , где – компакт

2. – достигает минимума и максимума на .

◄ 1) непрерывна , где функция локально ограничена .

Из покрытия выделяем конечное подпокрытие | < . Обозначим

2) Пусть , . Покажем, что . Предположим противное ограничена. В то же время и неограничена. ►

Теорема Больцано-Коши (о промежуточных значениях)

Определение 2.24. Путем в назовем непрерывное отображение , – носитель пути или параметризованная кривая.

Определение 2.25. Множество называется линейно связным, если , и с концами в точках Иными словами из любой точки множества можно непрерывно переместиться в любую другую точку этого множества, не выходя за его пределы.

Теорема 2.7 (Больцано-Коши). Пусть , линейно связно, , ,

.

◄ Т.к. линейно связно, : , Г( )=b,

Обозначим Поскольку Г, – непрерывны .

– по теореме Больцано-Коши в одномерном случае. Пусть

Тогда ►