29

Оглавление

ЛЕКЦИЯ №9 2

Глава 2. Дифференциальное исчисление функции многих переменных 2

как метрическое пространство 2

Открытые и замкнутые множества 3

ЛЕКЦИЯ №10 4

Компакты в 4

ЛЕКЦИЯ №11 5

Предел функции многих переменных 5

Общие свойства предела 6

ЛЕКЦИЯ № 12 8

Непрерывность отображения f : 8

Локальные свойства непрерывных отображений 8

Глобальные свойства непрерывных отображений 9

ЛЕКЦИЯ №13 10

Дифференциал функции многих переменных f : 10

ЛЕКЦИЯ №14 12

Производная по направлению. Градиент. 12

Касательная плоскость и нормаль к поверхности в R³ 13

ЛЕКЦИЯ №15 14

Частные производные высших порядков 14

Дифференциалы высших порядков 15

Нарушение инвариантности формы дифференциалов высшего порядка 16

ЛЕКЦИЯ №16 16

Формула Тейлора для функций многих переменных 16

Экстремум функций многих переменных 17

Достаточное условие экстремума 17

ЛЕКЦИЯ №17 19

Неявные функции 19

Теорема о неявной функции 19

ЛЕКЦИЯ №18 21

Дифференциал отображения f: 21

Свойства дифференциала отображения 22

ЛЕКЦИЯ №19 23

Теорема о системе неявных функций 23

Касательная плоскость к поверхности заданной неявно 24

ЛЕКЦИЯ № 20 24

Поверхность размерности k в 24

Касательное пространство 26

ЛЕКЦИЯ №21 27

Условный экстремум 27

Необходимый признак условного экстремума 27

Метод множителей Лагранжа 28

Достаточный признак условного экстремума 29

Лекция №9 Глава 2. Дифференциальное исчисление функции многих переменных как метрическое пространство

Определение 2.1. – множество, – метрика,

– метрическое пространство, если

1. 

2. 

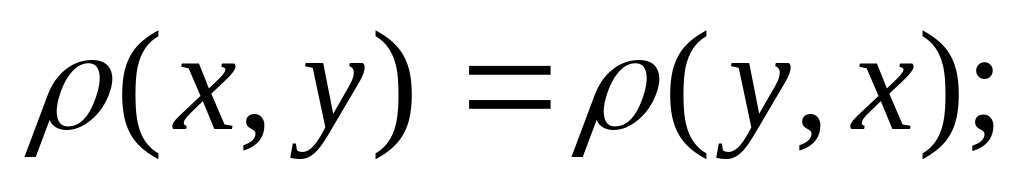
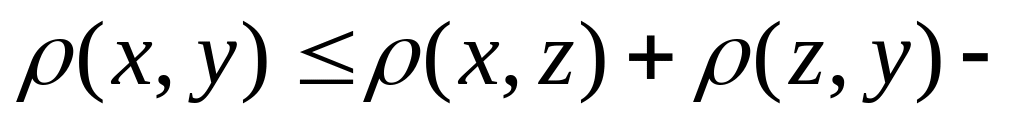3. неравенство треугольника.

Пространство

при метрика в

Зададим метрику в

Проверим выполнение свойств 1-3 метрики:

Свойства 1,2 следуют непосредственно из определения.

Для проверки 3 воспользуемся неравенством Коши – Буняковского (Шварца):

Утверждение 2.1 (неравенство Коши – Буняковского).

.

В координатной форме:

◄

В этом случае дискриминант ►

Следствие 2.1.

.

◄

►

Докажем свойство 3 метрики, используя следствие 2.1:

Открытые и замкнутые множества

Определение 2.2. – открытый шар в , .

Определение 2.3. Множество открытое, если

Определение 2.4. – замкнуто, если – открыто.

Пример 2.1. открытые множества.

При этом оба замкнутые.

Утверждение 2.2. – открытое.

◄ Возьмем и построим шар

Покажем, что

►

Утверждение 2.3. – открыто.

Утверждение 2.4. – замкнуто,

т.к.

Сфера:

замкнуто, т.к. сфера – граница шара

Утверждение 2.5. Пусть – открыто, – замкнуто

1. – открыто;

2. – открыто.

3. – замкнуто;

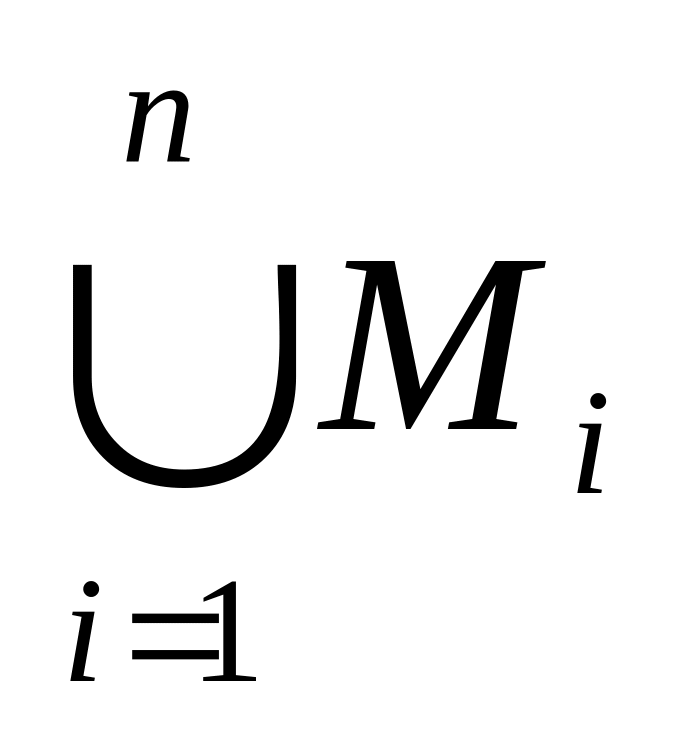4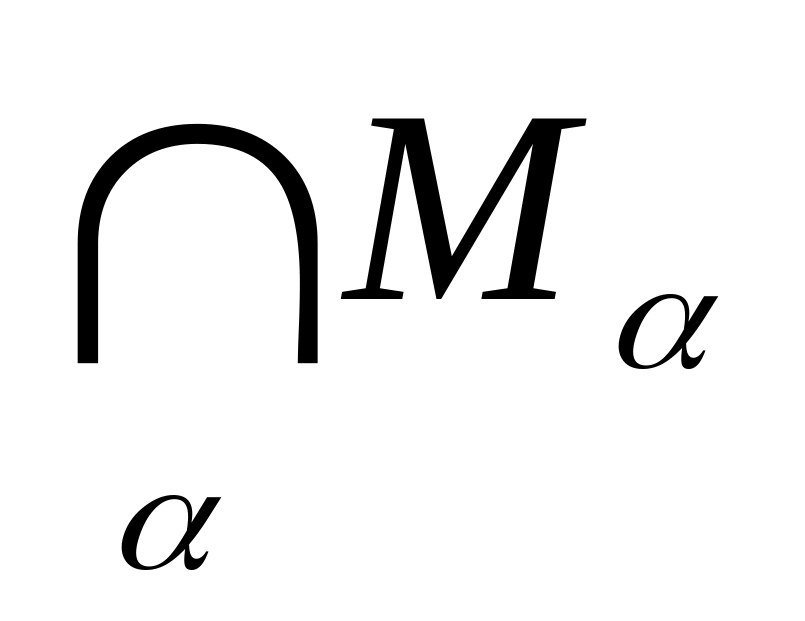. – замкнуто;

◄ 1) .

2)

пусть ,

3) Для замкнутых множеств: ,

– дополнения открытого замкнуто.

Аналогично 4). ►

Пример 2.2. Сфера: замкнута, т.к.

Определение 2.5. Окрестностью точки называют любое открытое множество, содержащее эту точку.

Определение 2.6. Точка х называется внутренней для множества , если она принадлежит вместе с некоторой окрестностью.

Определение 2.7. Точка х называется внешней для множества , если она внутренняя для \ .

Определение 2.8. Точка х называется граничной для множества , если она не является ни внутренней ни внешней, если в любой окрестности содержатся как точки множества так и точки \ .

Пример 2.3. открытое х внутренняя.

Пример 2.4. Для множеств граничными точками являются точки сферы . Сама сфера состоит только из граничных точек.

Пример 2.5.

точки – граничные.

точки – граничные.

Пример 2.6. – открытое множество.

Определение 2.9. Точка х называется предельной для множества ,

1) если в любой окрестности х содержится бесконечное множество точек ;

или

2) если любая окрестность х содержит хотя бы одну точку у , .

Определение 2.10. Множество вместе со своими предельными точками называется замыканием множества Е.

Пример 2.7.

Пример 2.8. в .

Утверждение 2.6. – замкнуто = .

◄ 1) Пусть замкнуто, тогда – открыто.

Возьмем точку , – открытое множество или окрестность , которая не содержит точек множества х – не предельная для х = .

2) = , тогда х

в которой нет точек , то есть x содержится в вместе со своей окрестностью – открыто – замкнуто. ►