Содержание

Введение………………………………………….........................1

1. Лабораторная работа №1…………………………...…………...2

2. Лабораторная работа №2………………………………………15

3. Заключение………………………………………………….…..18

Список использованной литературы…………………….……19

Введение

Курс «Математика» есть совокупность математических дисциплин, входящих в учебный план высших технических и некоторых специальных учебных заведений. Он знакомит с основными понятиями линейной алгебры, аналитической геометрии, математического анализа, математического и линейного программирования, теории вероятностей, математической статистики, служит базой для изучения общенаучных, общеобразовательных и специальных дисциплин. Модели и методы математики являются хорошим средством и языком для построения и анализа моделей в различных науках. Влияние информационных технологий затрагивает практически все стороны нашей жизни. Компьютеры буквально на глазах изменяют нашу жизнь. Появляются потребности в новых способах обработки информации и возникают новые информационные технологии, которые с каждым годом все активнее проникают в различные области знаний: экономику, управление, экологию и т.д.

Математика и ее методы стали обязательным предметом при подготовке специалистов любого профиля. Математика вросла в науки, став универсальным языком описания различных процессов и явлений. Огромный опыт человечества убедительно доказал, что математика является незаменимым и мощным орудием познания мира. С компьютеризацией всех областей человеческой деятельности pоль математических методов еще больше возрастает.

С помощью математических методов исследуются сложные прикладные задачи описательного, оптимизационного и управленческого типов, которые нельзя решить с помощью других более простых методов или основываясь только лишь на опыте и "здравом смысле".

В данных методических указаниях к выполнению лабораторных работ рассмотрены вопросы применения математических функций программы Microsoft Excel для решения типовых математических задач.

Лабораторная работа №1. Определители и матрицы

Цель работы: научиться выполнять действия над матрицами, решать матричные уравнения, используя для упрощения расчётов математические функции программы Microsoft Excel.

Задачи работы:

1. Даны матрицы А и В. Найти:

а) матрицу А + В;

б) матрицу 2B;

в) произведение A(A+B) матриц А и A+B;

г) матрицу (A+B)^-1 обратную к матрице A+B;

д) определитель матрицы A+B;

е) матрицу (A+2B)^T транспонированную к матрице A+2B.

2. Для данных матриц А и В решить матричное уравнение AX = B.

Ход работы

Для выполнения поставленных задач с помощью ЭВМ, целесообразно использовать табличный процессор Microsoft Excel 2007. С помощью различных математических формул, встроенных в данный программный продукт, возможно проводить математические расчеты с участием матриц. Данные для выполнения работы выбраны согласно необходимым критериям

Вариант №14

A= B=

Задача № 1

Найти сумму матриц А+B

Решение с помощью встроенных функций Excel выглядит так:

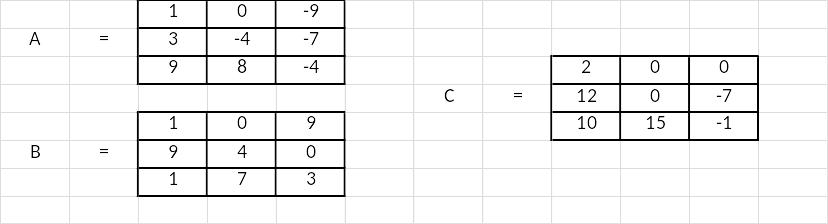
Здесь использована функция СУММ. Ее синтаксис таков: =СУММ([число]; [число]). С ее помощью складываются отдельные ячейки с данными.

Решение в режиме отображения формул:

Выполнение данного задания вручную выглядит примерно так:

С= =

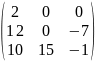
Задача № 2

Найти результат умножения матрицы B на число 2

Решение с помощью встроенных функций Excel выглядит так:

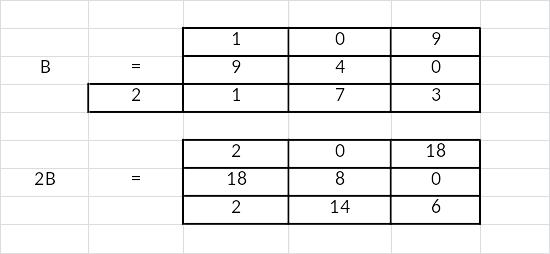
Решение в режиме отображения формул:

Выполнение данного задания вручную

2B= =

Задача № 3

Найти произведение A(A+B) матриц А и A+B;

Из задачи №1, решение для сложения двух матриц A и B с помощью Excel будет выглядеть так:

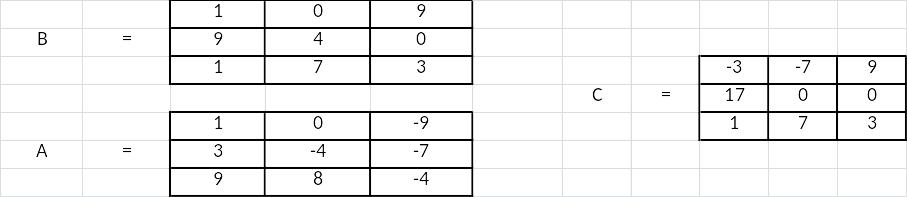
Затем производим умножение матрицы А на сумму матриц С:

В данной задаче была применена встроенная функция МУМНОЖ.

Синтаксис таков: =МУМНОЖ(массив1; массив2).

Данная функция возвращает матричное произведение двух массивов данных, причем результат имеет то же число строк, что и первый массив, и то же число столбцов, что и второй массив.

Вот так будет выглядеть решение в режиме отображения формул:

Выполнение данного задания вручную могло бы выглядеть примерно так:

А) Находим матрицу А+B (см. Задача №1);

Б) Находим матрицу А(А+B)

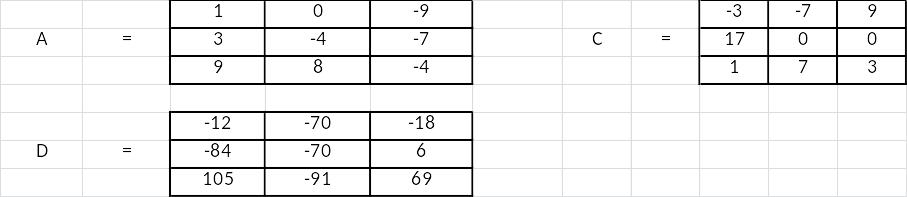
A= С =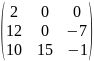

D= * =

=

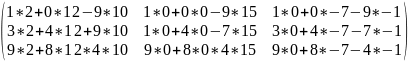
Задача № 4

Найти матрицу (A+B)^-1 обратную к матрице A+B;

Из задачи №1, решение для сложения двух матриц A и B с помощью Excel будет выглядеть так:

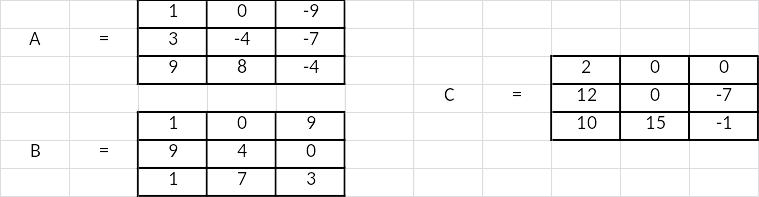
Находим матрицу, обратную матрице С и ее определитель:

Для нахождения обратной матрицы С, была использована функция МОБР. Ее синтаксис таков: =МОБР(массив). Данная функция возвращает массив данных, но с уже измененными значениями.

Для нахождения определителя матрицы С в данном случае была использована функция МОПРЕД. Синтаксис таков: =МОПРЕД(массив). С помощью этой функции можно быстро и точно рассчитать определитель матрицы.

Вот так будет выглядеть решение в режиме отображения формул:

Выполнение данного задания вручную могло бы выглядеть примерно так:

А) Находим матрицу А+B (см. Задача №1);

Б) Находим алгебраические дополнения к элементам матрицы С и составляем новую матрицу D:

C=

A₁₁= = 105; A₁₂= = -82; A₁₃= = 180;

A₂₁= = 0; A₂₂=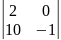 = -5; A₂₃= = 30;

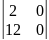A₃₁= = 0; A₃₂= = -14; A₃₃= = 0;

D=

В) Находим определитель матрицы С:

С| = 2 + 0 -7 = 210;

Г) Находим обратную матрицу D, путем умножения матрицы D на определитель матрицы С и округления получившихся значений:

=

Задача № 5

Найти определитель матрицы A+B;

Из задачи №1, решение для сложения двух матриц A и B с помощью Excel будет выглядеть так:

Находим определитель матрицы С:

Для нахождения определителя матрицы С в данном случае была использована функция МОПРЕД. Синтаксис таков: =МОПРЕД(массив). С помощью этой функции можно быстро и точно рассчитать определитель матрицы.

Вот так будет выглядеть решение в режиме отображения формул:

Выполнение данного задания вручную могло бы выглядеть примерно так:

А) Находим матрицу А+B (см. Задача №1);

Б) Находим определитель матрицы С:

С| = 2 + 0 -7 = 210;

Задача № 6

Найти матрицу (A+2B)^T транспонированную к матрице A+2B.

Из задачи №2 решение для умножения матрицы B на число 2 будет выглядеть так:

Решение для сложения двух матриц A и 2B с помощью Excel будет выглядеть так:

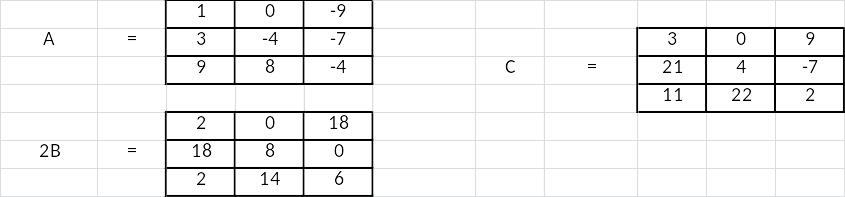
Здесь использована функция СУММ. Ее синтаксис таков: =СУММ([число]; [число]). С ее помощью складываются отдельные ячейки с данными.

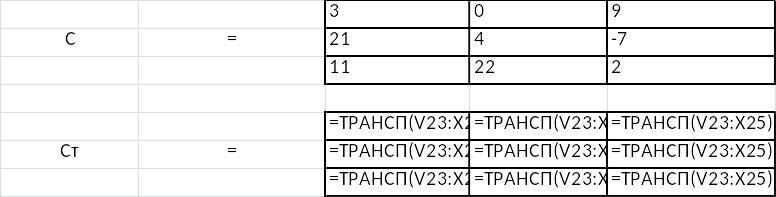
Находим транспонированную матрицу С:

В данном случае использовалась функция ТРАНСП. Ее синтаксис таков: =ТРАНСП(массив). С помощью этой функции можно быстро транспонировать матрицу.

Решение в режиме отображения формул:

Выполнение данного задания вручную могло бы выглядеть примерно так:

А) Находим матрицу 2B (см. Задача №2);

Б) Складываем матрицы (A+2B)

С= = ;

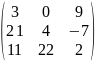В) Находим транспонированную матрицу С:

С=

Задача № 7

Для данных матриц А и В решить матричное уравнение A= AX = B

Путем решения буквенного уравнения, получаем AX=B –>

X=A(-1)B.

Из этого следует, что необходимо найти обратную матрицу А и умножить ее на матрицу B. Полученный результат и будет решением данного уравнения.

С помощью Excel, найдем обратную матрицу А:

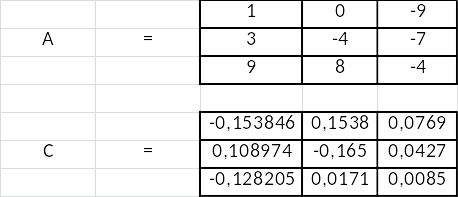
Для нахождения обратной матрицы С, была использована функция МОБР. Ее синтаксис таков: =МОБР(массив). Данная функция возвращает массив данных, но с уже измененными значениями.

Решение для умножения двух матриц С и B с помощью Excel будет выглядеть так:

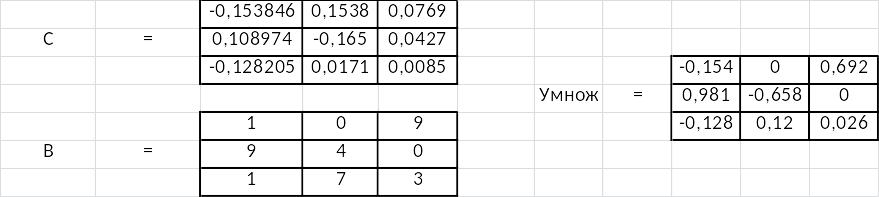
Здесь использован символ *, который означает умножение числа на число. Ее синтаксис таков: =[число]*[число]. С помощью данного символа возможно умножать не только отдельные ячейки, но также и целые массивы данных.

Решение в режиме отображения формул:

Таким образом, найдена матрица Х

Х=

Выполнение данного задания вручную могло бы выглядеть примерно так:

А) Находим определитель матрицы С:

С= = |С| = 1 + 0 + 9 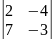= 182;

Б) Находим обратную матрицу С:

С= = ;

В) Умножим матрицу С на матрицу B и получим ответ в виде матрицы Х:

B= ; С=

Х= =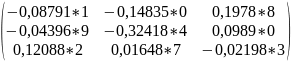

= .