Задание 1.
1. Преобразовать исходную выборку в статистический группированный ряд.
2. Представить выборки наблюдений в виде таблицы частот, используя N интервалов группировки. Число N определить по формуле Стэрджеса.
3. Построить полигон и гистограмму относительных частот.
3. Вычислить выборочные характеристики изучаемого признака для не группированных и группированных выборок: среднее, дисперсию, среднее квадратическое (стандартное) отклонение, центральный момента 3-го порядка; центральный момента 4-го порядка; асимметрия; эксцесс, мода, медиана.
4. На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
5. Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.4 закону распределения при уровне значимости 0,05.
6. Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,95.
7. С надежностью 0,95 проверить гипотезу о равенстве:
а) генеральной
средней значению
;
б) генеральной дисперсии значению 0,25С 2, где С = 1 + (К + М)/100.
В выражениях для данных используются следующие обозначения: К и М – предпоследняя и последняя цифры соответственно зачетной книжки.
ЗАДАНИЕ 2.
Построить поле корреляции (точечную диаграмму), изобразив в прямоугольной системе координат точки с координатами, соответствующими каждой паре наблюдений (xi yi).
На основании поля корреляции сделать предположение о наличии между случайными величинами X (выборка 1) и Y (выборка 2) корреляционной зависимости и о форме этой зависимости (линейная или нелинейная).
Вычислить оценки математических ожиданий случайных величин X и Y - средние арифметические
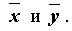
Вычислить оценки средних квадратических отклонений
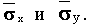
Вычислить оценку коэффициента корреляции r - выборочный коэффициент корреляции.
Проверить гипотезу о равенстве нулю генерального коэффициента корреляции.
Оценить надежность коэффициента корреляции ( критерий Фишера).
Получить уравнение регрессии случайной величины Y на X. Нанести прямую регрессии на график.
Оценить точность регрессии.
Выполнить точечную и интервальную оценку точности параметров уравнения регрессии.
Сделать общий вывод по результатам анализа.
ЗАДАНИЕ 3. По данным двух выборок проверить гипотезы о значимости
выборочного рангового коэффициента Спирмена и Кендалла при уровне значимости α. В ответе привести:
1) выборочный коэффициент ранговой корреляции Спирмена;
2) выборочный коэффициент ранговой корреляции Кендалла;
3)
критическую точку для коэффициента
Спирмена
;
4)
критическую точку для коэффициента
Кендалла
;
5) вывод о принятии или не принятии каждой гипотезы.
Вариант №1
Выборка 1:
139.3 31.2 131.2 112.1 54.0 77.3 24.9 106.0 96.4 22.2 92.8 111.0 49.6 61.3 95.9 52.1 124.0 57.8 99.5 71.0 79.3 99.6 133.9 1.7 122.0 41.3 27.0 -6.7 27.8 60.8 78.6 171.0 78.4 56.7 50.0 46.3 91.6 151.7 115.4 21.9 42.8 78.0 114.9 91.2 107.8 100.9 97.0 52.3 34.4 49.1 111.6 77.4 1.2 28.0 55.7 58.0 55.1 41.5 97.1 81.9 48.3 113.9 33.3 41.5 50.2 148.5 45.0 98.3 7.9 75.3 67.3 106.5 65.9 104.4 17.1 63.9 108.5 58.6 33.0 115.5 -13.3 60.3 71.1 56.3 34.9 61.5 65.2 71.8 87.4 57.8 63.1 56.9 126.0 90.9 70.6 132.5 86.3 108.2 82.0 56.4
Выборка 2:
116.0 65.5 115.1 89.5 62.7 92.7 63.9 71.8 73.7 70.1 88.6 81.5 70.5 102.8 76.8 83.2 105.0 88.5 85.5 105.6 54.6 85.5 60.1 76.8 47.8 48.3 119.7 109.4 42.6 46.1 43.0 53.1 86.3 65.4 61.0 21.1 59.7 70.1 101.9 59.4 70.0 53.7 59.5 82.3 111.8 74.3 52.9 82.5 86.4 49.1 112.8 83.1 69.1 39.1 42.0 40.1 37.8 76.7 74.7 118.7 65.4 84.1 54.9 13.5 23.4 75.8 87.4 56.9 48.9 35.0 66.0 98.0 81.6 91.2 74.3 87.4 81.6 80.9 47.3 62.1 65.2 57.1 31.0 81.4 81.7 42.2 93.1 62.4 65.7 87.9 67.0 65.3 64.2 69.5 78.5 111.8 38.7 54.2 56.3 63.0