КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Прогнозирование

национальной экономики»

Вариант 4

Содержание:

Задание 1. 3

Задание 2. 10

Список использованной литературы 15

Задание 1.

Имеются данные численности наличного населения города Г за 1999–2007 гг. (на начало года), тыс. чел.

1999	2000	2001	2002	2003	2004	2005	2006	2007
106,8	106	105,4	103	102,8	102,7	102,7	102,6	102,5

1. Постройте прогноз численности наличного населения города Г на 2008-2010 гг., используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.

2. Постройте график фактического и расчетных показателей

3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.

4. Сравните результаты.

Решение:

Метод скользящей средней.

Определим величину интервала сглаживания, например равную 3 (n=3).

Годы	Численность населения города, тыс. чел. y1	Скользящая средняя m	Расчет средней относительной ошибки |y1-m|*100 Y1
1999	106,8	-	-
2000	106	106,1	0,1
2001	105,4	104,8	0,6
2002	103	103,7	0,7
2003	102,8	102,8	0
2004	102,7	102,7	0
2005	102,7	102,7	0
2006	102,6	102,6	0
2007	102,5	-
Итого	934,5		1,4
Прогноз
2008	102,6	102,6
2009	102,6
2010	102,6

Рассчитаем скользящую среднюю для первых трех периодов.

M₂₀₀₀=(y₁₉₉₉+y₂₀₀₀+y₂₀₀₁):3= (106,8+106,0+105,4):3=106,1

М₂₀₀₁=(y₂₀₀₀+y₂₀₀₁+y₂₀₀₂):3=(106,0+105,4+103,0):3=104,8

Рассчитав скользящую среднюю для всех периодов, строим прогноз на 2008-2010 г.

y₂₀₀₈=102,6+1/3*(102,5-102,6)=102,6-0,03=102,6

Определяем скользящую среднюю m для 2007 г.

m= (102,6+102,5+102,6):3=102,6

Строим прогноз на 2009 г.

y₂₀₀₉=102,6+1/3*(102,6-102,5)=102,6

Определяем скользящую m для 2008 г.

m=(102,5+102,6+102,6):3=102,6

Рассчитываем среднюю относительную ошибку:

є =1,4:7=0,2%

Вывод:

По расчетам прогноза видно, что численность населения практически не меняется и составляет в среднем 102,6 тыс.чел. Так как средняя относительная ошибка равна 0,2%, то точность данного прогноза является высокой.

Метод экспоненциального сглаживания.

Определяем значение параметра сглаживания:

α = 2/(n+1)=2/(9+1)=0,2

Определяем начальное значение U₀ двумя способами:

I способ (средняя арифметическая) U₀ =934,5 : 9=103,8;

II способ (принимаем первое значение базы прогноза) U₀ =106,8.

Рассчитываем экспоненциально взвешенную среднюю для каждого года, используя формулу

y_t+1= α  y_t+(1- α) U_t.

I способ: U₂₀₀₀ =106,8*0,2+(1-0,2)*103,8=104,4

U₂₀₀₁ =106*0,2+(1-0,2)*104,4=104,7

U₂₀₀₂ =105,4*0,2+(1-0,2)*104,7=104,9

U₂₀₀₃ =103*0,2+(1-0,2)*104,9=104,5

U₂₀₀₄ =102,8*0,2+(1-0,2)*104,5=104,2

U₂₀₀₅ =102,7*0,2+(1-0,2)*104,2=103,9

U₂₀₀₆ =102,7*0,2+(1-0,2)*103,9=103,6

U₂₀₀₇ =102,6*0,2+(1-0,2)*103,6=103,4

Составим таблицу.

Годы	Численность населения города, тыс. чел. y1	Экспоненциально взвешенная средняя Ut		Расчет средней относительной ошибки
		I Способ	II Способ	I Способ	II Способ
1999	106,8	103,8	106,8	2,8	0,0
2000	106	104,4	106,8	1,5	0,8
2001	105,4	104,7	106,6	0,6	1,2
2002	103	104,9	106,4	1,8	3,3
2003	102,8	104,5	105,7	1,7	2,8
2004	102,7	104,2	105,1	1,4	2,4
2005	102,7	103,9	104,6	1,1	1,9
2006	102,6	103,6	104,3	1,0	1,6
2007	102,5	103,4	103,9	0,9	1,4
Итого	934,5	937,5	950,3	12,8	15,3
Прогноз
2008		103,2	103,6
2009		103,1	103,4
2010		103	103,2

II способ: U₁₉₉₂ =106,8*0,2+(1-,02)*106,8=106,8

U₁₉₉₃ =106*0,2+(1-,02)*106,8=106,6

U₁₉₉₄ =105,4*0,2+(1-,02)*106,6=106,4

U₁₉₉₅ =103*0,2+(1-,02)*106,4=105,7

U₁₉₉₆ =102,8*0,2+(1-,02)*105,7=105,1

U₁₉₉₇ =102,7*0,2+(1-,02)*105,1=104,6

U₁₉₉₈ =102,7*0,2+(1-,02)*104,6=104,3

U₁₉₉₉ =102,6*0,2+(1-,02)*104,3=103,9

Рассчитываем прогнозное значение, используя формулу

y_t+1= α  y₂₀₀₇+(1- α) U_t.

I способ: U₂₀₀₈=102,5*0,2+0,8*103,4=103,2

U₂₀₀₉=102,5*0,2+0,8*103,2=103,1

U₂₀₁₀=102,5*0,2+0,8*103,1=103

II способ: U₂₀₀₈=102,5*0,2+0,8*103,9=103,6

U₂₀₀₉=102,5*0,2+0,8*103,6=103,4

U₂₀₁₀=102,5*0,2+0,8*103,4=103,2

Средняя относительная ошибка

є

I способ: є =12,8:9=1,4%

II способ: є =15,8:9=1,7%

Вывод:

По рассчитанной средней относительной ошибке видно, что наиболее точность прогноза по методу экспоненциальной взвешенной наблюдается в первом способе расчета (є=1,4), т.е. по средней арифметической.

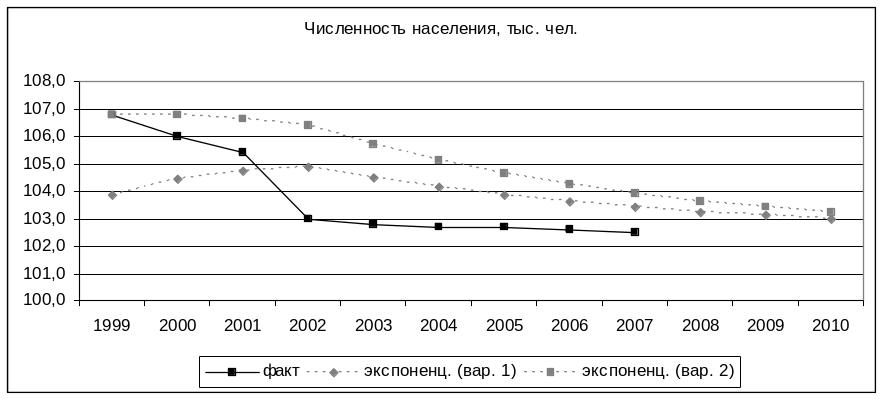
Метод наименьших квадратов.

Для решения используем следующую таблицу.

Годы	Численность населения города, тыс. чел. y1	Условное обозначение времени Х	y1*X	х2	m	Расчет средней относительной ошибки
1	2	3	4	5	6	7
1999	106,8	1	106,8	1	106,0	0,7
2000	106	2	212	4	105,5	0,5
2001	105,4	3	316,2	9	104,9	0,4
2002	103	4	412	16	104,4	1,3
2003	102,8	5	514	25	103,8	1,0
2004	102,7	6	616,2	36	103,3	0,6
2005	102,7	7	718,9	49	102,7	0,0
2006	102,6	8	820,8	64	102,2	0,4
2007	102,5	9	922,5	81	101,6	0,9
Итого	934,5	45	4639,4	285	934,5	5,8
Прогноз
2000	101,1	10
2001	100,5	11
2002	100,0	12

Определим условное обозначение времени как последовательную нумерацию периодов базы прогноза. Рассчитаем графы 4 и 5.

m определим по формуле y_t+1 = aX+b, а коэффициенты a и b по формулам:

a = 4639,4-(45*934,5)/9 = -0,55

285-45²/9

b = 934,5/9-(-0,6)*45/9 =106,6

y ₁₉₉₉ =-0,55*1+106,6=106,0

y ₂₀₀₀ =-0,55*2+106,6=105,5

y ₂₀₀₁ =-0,55*3+106,6=104,9

y ₂₀₀₂ =-0,55*4+106,6=104,4

y ₂₀₀₃ =-0,55*5+106,6=103,8

y ₂₀₀₄ =-0,55*6+106,6=103,3

y ₂₀₀₅ =-0,55*7+106,6=102,7

y ₂₀₀₆ =-0,55*8+106,6=102,2

y ₂₀₀₇ =-0,55*9+106,6=101,6

Определяем прогнозное значение.

y₂₀₀₈=-0,55*10+106,6=101,1

y₂₀₀₉=-0,55*11+106,6=100,5

y₂₀₁₀=-0,55*12+106,6=100,0

Рассчитываем среднюю относительную ошибку

є

є=5,8:9=0,6%

Вывод:

По рассчитанному прогнозу видно, что численность населения имеет тенденцию к снижению, также из расчета средней относительной ошибки можно определить, что точность прогноза является высокой, так как её значение ниже 10%.

Общий вывод по заданию №1:

Наиболее точным является метод скользящей средней, здесь наблюдается наименьшее значение по расчету средней относительной ошибки, значение расчета = 0,2%. Если сравнивать графики, то линия расчета по методу скользящей является наиболее приближенной к фактическим значениям, что является основанием предполагать, что данный прогноз наиболее верен из всех остальных. Оценивая наиболее точный демографический прогноз, то по его данным население города будет сохраняться на одном уровне, в среднем оно будет составлять 102,6 тыс.человек.