Задачи, приводящие к понятию функции нескольких переменных
Во многих процессах и явлениях, встречающихся в природе, в практической деятельности человека, числовые значения одной величины определяются набором из двух, трех и большего количества независимых переменных. При изучении подобных зависимостей используют понятие функции нескольких переменных.
Обратимся к задачам, приводящим собственно к этому понятию.
Задача 1: Если через х и у обозначить длины сторон прямоугольника, то его площадь S выражается формулой S=xy. При изменении х и у меняется и площадь S. В этом случае говорят, что площадь S есть функция двух переменных х и у, заданная формулой S=xy.
Задача 2: Дальность d
полета тела, брошенного с начальной
скоростью
под углом
к горизонту, также является функцией
двух переменных
и
и задается формулой
,
где g – ускорение силы
тяжести.
Задача 3: Объем V прямоугольного параллелепипеда с ребрами, длины которых равны x, y и z, является функцией трех переменных x, y и z и задается формулой V=xyz.
Задача 4: При изучении свойств нагретого тела его температура рассматривается обычно переменной величиной, зависящей от точки, в которой измеряется температура, и от момента времени, в который проводится измерение.
Если точка имеет координаты (x;y;z),
тогда зависимость температуры Т от
координат точки и момента времени t
обозначается следующим образом:
,
то есть температура Т является
функцией четырех переменных. Переменные
x, y,
z, t
– независимые переменные, они могут
принимать любые допустимые значения.
Переменная Т является зависимой
переменной, значения которой определяются
значениями независимых переменных x,
y, z,
t.
В дальнейшем остановимся на подробном изучении функции двух переменных, так как все важнейшие факты теории функции нескольких переменных наблюдаются уже на функциях двух переменных. Распространение определений и полученных результатов на функции трех и более переменных представляет собой, как правило, лишь технические трудности.
Понятие функции двух действительных переменных
Соответствие
,
которое каждой паре значений переменных
х и у, принадлежащей некоторому
множеству пар D,
сопоставляет единственное число
,
называется функцией двух переменных,
определенной на множестве D
со значениями в
.
Символически функция двух переменных
обозначается следующим образом:
.
При этом х и у называются
независимыми переменными
(аргументами), а z –
зависимой переменной
(функцией).
Множество D пар значений, которые могут принимать независимые переменные х и у (значение функции при этом является числом), называется областью определения функции двух переменных.
Для различных функций двух переменных область определения имеет разный вид. Она может представлять собой конечную или бесконечную часть плоскости, ограниченную одной или несколькими непрерывными линиями – границами области. Возможен случай, когда какая – то из границ превращается в одну точку. Так, областью определения функции S=xy из задачи 1 с учетом ее геометрического смысла является множество точек плоскости первой координатой четверти за исключением точек осей координат:
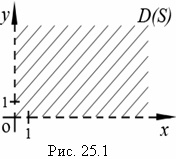
(рис. 25.1).
Множество всех значений, принимаемых в области ее определения, называется областью значений функции и обозначается Е.