ЛЕКЦІЯ № 29(7.2) З ДИСЦИПЛІНИ

«ОСНОВИ ТЕОРІЇ ЗАХИСТУ ІНФОРМАЦІЇ»

Тема лекції

Методи криптоаналізу дискретних логарифмів в полі f(p) Навчальні питання

29.1 (7.2.1) Методи дискретного логарифмування в скінченному полі Галуа F(q)

29.2 (7.2.2) . Дискретне логарифмування методом ρ - Полларда

29.3 (7.2.3) Метод Поліга-Геллмана дискретного логарифмування

29.4 (7.2.4). Решето числового поля для дискретного логарифмування

29.5 (7.2.5) Порівняння складності дискретного логарифмування

29.5(7.2. 5). Квантовий алгоритм факторизації цілих чисел

Додаток А Стійкість асиметричних криптосистем, що базуються на крипто перетвореннях в простих полях. Приклади розв’язку задач та задачі для самостійного розв’язання

ОСНОВНІ ДЖЕРЕРЛА.

1. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Монографія Розд 9. Харків, ХНУРЕ, 2012 р.

2. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний конспект лекцій. (ЛК №28). Харків, ХНУРЕ, 2012 р.

3. Горбенко І. Д. Гриненко Т. О. Захист інформації в інформаційно-телекомунікаційних системах: Навч. посібник. Ч.1. Криптографічний захист інформації - Харків: ХНУРЕ, 2004 - 368 с.

4. Горбенко Ю.І., Горбенко І.Д. Інфраструктури відкритих ключів . Системи ЕЦП. Теорія та практика. Харків. Форт. 2010 , 593с.

Додаткові джерела

1.В. Задірака . Компьютерная криптологія. Підручник. К, 2002 ,504с.

2. А. Менезис, П. Ван Аршот, С. Ватсон. Руководство по прикладной криптографии CRC Press, 1997, электронная копия, 662 с

3. Брюс Шнайер. Прикладная криптография. М., изд. Триумф. 2002 г., 797 с

4. Закон України « Про електронний цифровий підпис»

Матеріал лекції

29.1 (7.2.1) Методи дискретного логарифмування в скінченному полі Галуа f(q)

На цей час відомі й доступні дві основні групи методів дискретного логарифмування в скінченному полі Галуа F(q) [4, 5, 11–13, 422, 426], що мають субекспоненційну та експоненційну складність.

До методів, що мають експоненційну складність, необхідно віднести:

- ρ-Полларда метод з евристичною оцінкою складності О(Р^1/2);

- метод Поліга-Геллмана, що може бути застосований, якщо відомий канонічний розклад числа Р–1;

- метод Шенкса (малих і великих кроків).

До методів, що мають субекспоненційну складність, необхідно віднести:

- метод Адлемана (запропонований ще в 1979 р.);

- метод Купершмідта (Don Coppersmith) або COS метод (запропонований у 1986 р.);

- решето числового поля (запропоноване Д. Гордоном у 1993 р.).

Розглянемо загальну постановку розв’язання задачі дискретного логарифмування в скінченному полі Галуа та основні методи розв’язання, що мають відповідно експоненційну та субекспоненційну складність. Також зведемо оцінки складності дискретного логарифмування до таблиці, що наведена в п.9.3.4.

29.2 (7.2.2) . Дискретне логарифмування методом ρ - Полларда

Нехай – примітивний елемент скінченного поля Галуа F(P) і Р – просте число. Тоді для кожного х_i (0 < x_i < P) існує однозначний х_i елемент поля :

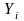(9.32)

і навпаки – для кожного _{існує однозначний хi}.

_Пара є асиметричною парою ключів криптоперетворення в скінченному полі Галуа, при чому х_i – особистий (конфіденційний) ключ, а Y_i – відкритий. Задача дискретного логарифмування зводиться до знаходження особистого ключа х_i при відомих загальних параметрах (Р, ) та відкритому ключі Y_i, тобто

. (9.33)

Розглянемо розв’язання (9.32)–(9.33) методом ρ-Полларда у загальному вигляді

. (9.34)

Рис. 9.2. Крива ρ-Полларда дискретного логарифмування створення колізії

Першим методом дискретного логарифмування, очевидно, був метод ρ-Полларда (рис. 9.2). Нехай необхідно розв’язати дискретне логарифмічне рівняння (9.34) відносно Х. За своєю сутностю метод ρ-Полларда дискретного логарифмування аналогічний методу факторизації [див. п.9.2.3]. Розглянемо його детально в дещо узагальненій постановці.

Сформуємо випадкові пари цілих чисел та . Нехай знайдено такі дві пари чисел та , що

. (9.35)

Підставимо (9.34) в (9.35), у результаті маємо:

або

. (9.36)

У порівнянні (9.36), згідно з теоремою Ойлера, степені можна прирівняти за модулем (Р-1), тобто

. (9.37)

Із (9.37), у свою чергу, маємо:

або

. (9.38)

Таким чином, із (9.38) випливає, що необхідно знайти пари цілих чисел і , що задовольняють (9.35), а далі, підставивши їх в (9.38), отримаємо розв’язок. По суті, алгоритм ρ-Полларда і забезпечує формування цих пар чисел.

Наступним кроком є вибір способу формування випадкових пар чисел _. Для цього, відповідно з рекомендаціями [5, 13, 425], виберемо в якості початкового елемент послідовності

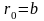. (9.39)

Далі будемо обчислювати послідовність за рекурентним правилом:

(9.40)

Постійну с вибирають таким чином, щоб вона перебувала між а та b приблизно на однаковій відстані. Але в більшості випадків її підбирають.

Послідовність називають послідовністю ρ-Полларда. Для успішного розв’язання дискретного логарифмічного рівняння необхідно знайти два значення та 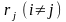– таких, що

. (9.41)

Після цього знаходимо значення і та обчислюємо згідно з (9.38) особистий ключ.

Рис. 9.3. Алгоритм створення колізії

Якщо правило або залежність 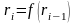буде рандомізованим, то ймовірність колізії за аналогією з [5, 12, 13], з урахуванням рис. 9.3, визначається параметричним рівнянням:

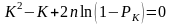_, (9.42)

при

_(9.43)

або

, (9.44)

де К – число експериментів згідно з рис. 9.3;

n – кількість можливих значень r_i;

– ймовірність виникнення колізії.

Для оцінки складності К потрібно задати два параметри: та .

Приклад 9.3. Розв’язати дискретне логарифмічне рівняння вигляду методом ρ-Полларда.

Розв’язання.:

Обчислимо значення з урахуванням того, що :

Виберемо С=6 та розрахуємо значення . Результати зведемо до таблиці 9.6.

Таблиця 9.6

Результати розрахунків при розв’язанні дискретного логарифмічного рівняння

І	1	2	3	4	5	6	7
ri	b=9	ab=20	a2b=1	a2b2=9	a3b2=20	a4b2=1	a4b3=9
Ui	0	1	2	2	3	4	4
Vi	1	1	1	2	2	2	3

Аналізуючи значення , бачимо, що r₁= r₄= r₇, r₂= r₅, r₃= r₆. Вибравши будь-яку пару та , знайдемо пари значень та . Наприклад, для r₃=r₆ маємо: для r₃ – U_i=2 та V_i=2; для r₆ – U_j=4 та V_j=3. Підставивши ці значення у (2.79), маємо:

.

Далі знайдемо зворотний елемент y для числа 21 у кільці за модулем 22. Маємо порівняння:

.

Розв’яжемо його, використовуючи алгоритм Евкліда:

Отже, тоді

Тому

Таким чином, Прямим обчисленням перевіряємо правильність розв’язку.

Приклад 9.4. Розв’язати методом ρ-Полларда порівняння 20 7^x (mod 23).

Обчислимо (9.38) таким чином:

де c = 10, r0 = b = 20, a = 7.

Розв’язання.

Таким чином, r₈ = r₀, причому r₈ можна подати як