Аналого-цифровий перетворювач

Передача інформації здійснюється з використанням дискретної системи зв'язку. Для цього повідомлення a(t) аналого-цифровим перетворювачем дискретизується за часом і квантується за рівнем.

Визначимо інтервал дискретизаціі за теоремою Котельнікова:

.

Визначимо кількість рівнів квантування L, потрібних для заміни будь-якого неперервного відліку a(t_i) квантованим відліком

;

.

Оскільки миттєві значення рівноймовірні в заданому інтервалі, то закон розподілу шуму W(ξ) в інтервалі a_j-Δa/2 ≤ ξ ≤a_j+Δa/2 буде рівноймовірним і не залежатиме від номера інтервалу.

Отже, середня потужність шуму квантування буде дорівнювати:

.

Закон розподілу шуму визначимо з умов нормування:

G_a(f) F_v N_a 4f

Тоді середня потужність шуму квантування:

;

;

.

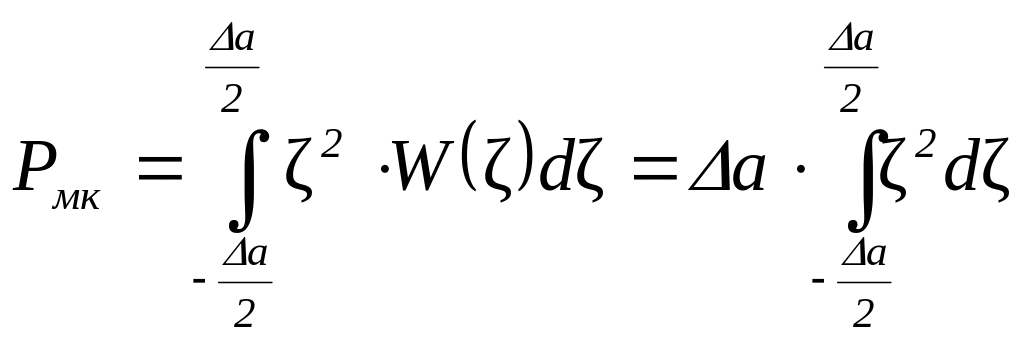Відносну величину потужності шуму квантування визначимо, використавши співвідношення Р_мк до дисперсії випадкового процесу a(t):

.

Мінімальна кількість двійкових розрядів (k), потрібна для запису в вигляді двійкового числа будь-якого номера з L номерів рівнів квантування, дорівнює:

.

Наприклад, представимо j = 29 в двійковій системі (рис. 5.)

j = 11101

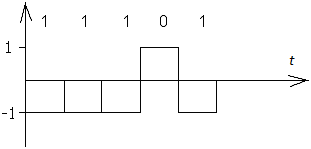
Рис. 5. Часова діаграма відгуку АЦП на рівень j

Ентропія H повідомлення (міра невизначеності):

імовірність потрапляння a(t) в інтервал дорівнює:

.

При заданому законі розподілу миттєвих значень процесу a(t) усі рівні квантування рівноймовірні, тому що P(a_i) не залежать від i.

Тоді ентропія визначатиметься як ентропія дискретного джерела незалежних повідомлень, усі символи якого рівноймовірні:

біт/символ.

Продуктивністю такого джерела буде сумарна ентропія повідомлень, переданих за одиницю часу:

.

Кодер

Кодер виконує систематичне кодування з однією перевіркою на парність, утворюючи код (n,k).

Сформулюємо правило кодування з перевіркою на парність.

Визначимо перевірний символ в₆ шляхом складання за модулем 2 усіх к=5 інформаційних символів:

правило складання за модулем 2 має вигляд:

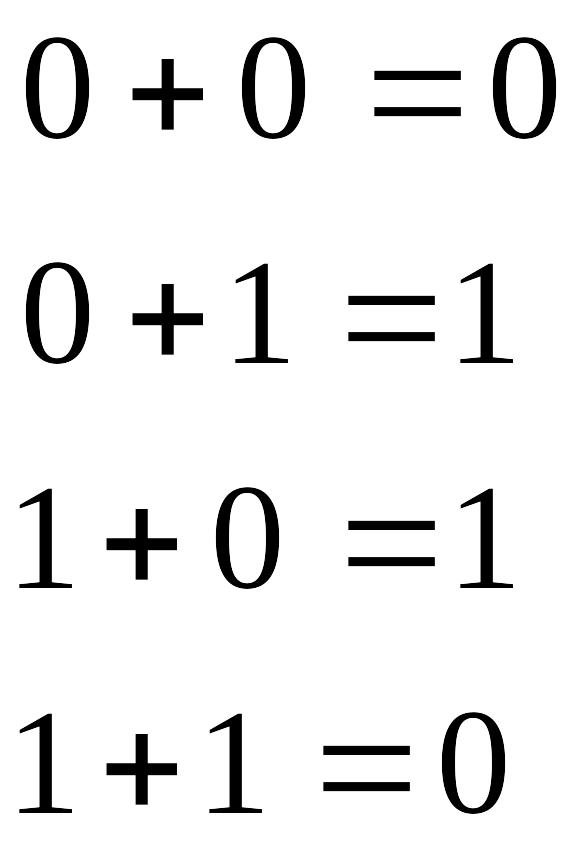
для числа j: в₆ = 1.

Надлишковість коду с однією перевіркою на парність

.

Двійкове кодове слово, утворене в результаті кодування двійкового числа з перевіркою на парність:

в₁ в₂ в₃ в₄ в₅ в₆

1 1 1 0 1 1

Інформаційні Перевірні

символи символи

Рис. 6. Імпульсна послідовність b(t)

Кількість двійкових символів, виданих кодером за секунду V_к, визначається кількістю відліків (1/Δt) і кількістю двійкових символів n=к+1, що припадають на один відлік.

Тривалість двійкового символу як величина зворотна V_k

.

Частотний модулятор

Наведемо вираз функції кореляції B_b(τ) модульованого сигналу b(t) (рис. 6.).

Для цього розглянемо два перерізи в моменти t₁ та t₂ (t₂-t₁=τ) і знайдемо математичні сподівання добутку X(t₁)X(t₁+τ).

Якщо τ>Т, то ці перерізи належать різним тактовим інтервалам, а добуток може з рівною імовірністю набувати значення +1 і -1, таким чином, доти його математичне сподівання дорівнювало б 0.

Якщо τ<Т, то можливі два випадки: випадок А, коли вони належать одному інтервалу і, отже, X(t₁)X(t₁+τ)=1, і випадок Б, коли вони належать різним тактовим інтервалам та X(t₁)X(t₁+τ) може з рівною ймовірністю дорівнювати +1 і -1. Тому при τ<Т математичне сподівання X(t₁)X(t₁+τ) дорівнює ймовірності р(а) того, що обидва перерізи виявляться в одному інтервалі. Випадок А має місце, якщо перший з двох перерізів спізнюється від початку тактового інтервалу не більше ніж Т-|τ|, а ймовірність цього дорівнює (Т - |τ|)/Т.

Тоді функція кореляції має вигляд:

Рис.7. Функція кореляції

Знайдемо вираз для спектральної щільності потужності модульованого сигналу G_b(f) за теоремою Віннера-Хінчіна:

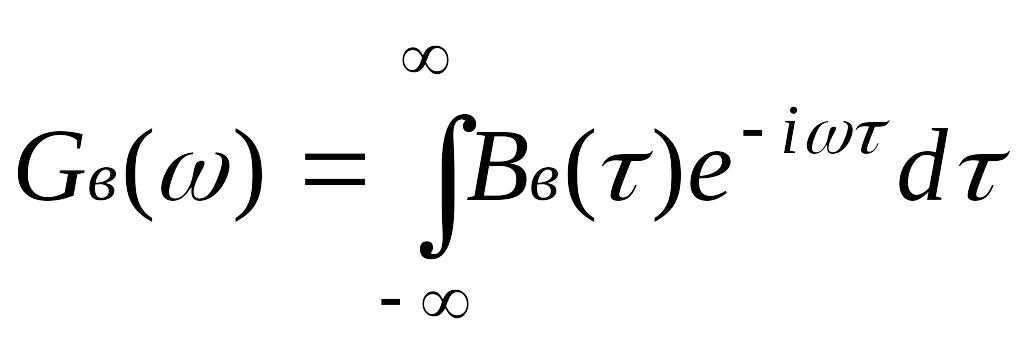
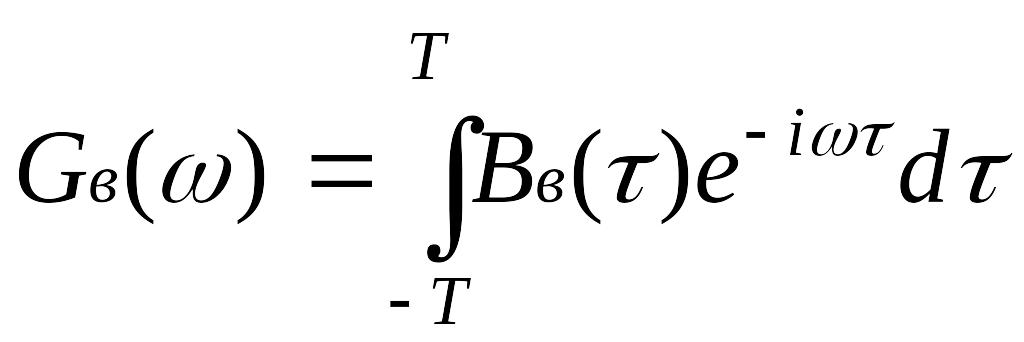
Оскільки В(τ) - функція парна, то:

;

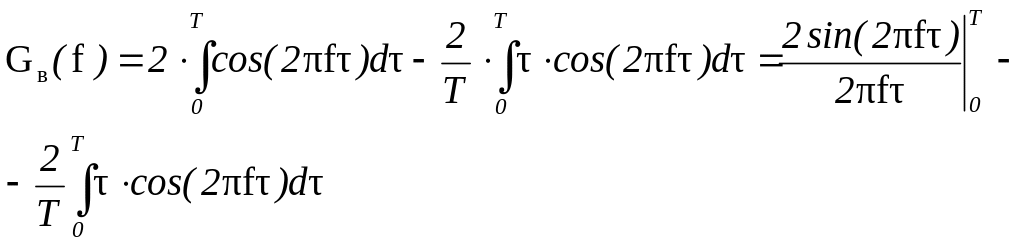
Візьмемо інтеграл по частинах:

.

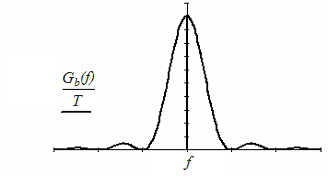
Рис.8. Графік спектральної щільності потужності модулюючого сигналу

Обмежимо верхню частоту ширини спектра модулюючого сигналу частотою F_b, при цьому знехтуємо спотвореннями, які виникають у часовій області

.

Визначимо частину потужності, зосереджену в смузі частот від 0 до :

;

.

Візьмемо цей інтеграл по частинах:

;

; ;

; ;

;

.

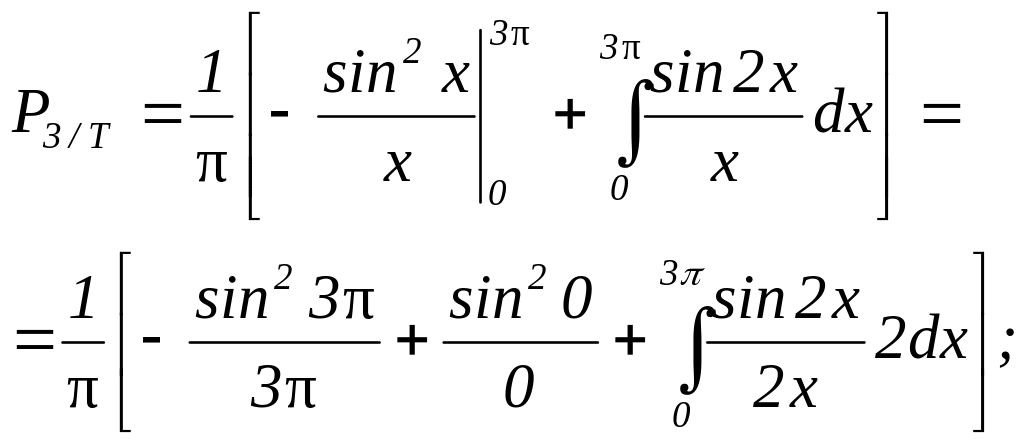
Отримуємо відсоток потужності сигналу який припадає на смугу частот від 0 до F_В.

Задана фазова маніпуляція, тобто

; .

Рис.9. Часові діаграми залежності сигналу s(t) від сигналу b(t) в разі передавання рівня з номером j.

П ри ЧМ вираз енергетичного спектра модульованого сигналу (рис. 10.) має вигляд:

Рис.10 Графік енергетичного спектра модульованого сигналу G_s(f)

Умовна ширина енергетичного спектра буде в два рази більша від умовної ширини енергетичного спектра модулюючого сигналу,