
- •О.В. Савилова Гидромеханика
- •Оглавление
- •Тема 1. Жидкости и газы, их свойства________________8
- •Тема 2. Гидростатика______________________________19
- •Тема 3 Основы гидродинамики______________________43
- •Тема 4 Ламинарное течение жидкости в круглых
- •Тема 5 Турбулентное течение жидкости в круглых
- •Тема 6 Местные гидравлические сопротивления_______81
- •Тема 7 Истечение жидкости через отверстия и насадки_89
- •Тема 8 Гидравлический расчет трубопроводов________99
- •Введение
- •Тема 1 Жидкости и газы, их свойства
- •Определение жидкости
- •Основные свойства жидкостей и газов
- •Силы, действующие в жидкости
- •Тема 2 Гидростатика
- •2.1 Гидростатическое давление и его свойства
- •2.2. Основное уравнение гидростатики
- •2.3 Закон Паскаля и его техническое применение
- •2.4 Дифференциальные уравнения Эйлера равновесия жидкости
- •2.5 Абсолютное и избыточное давление. Вакуум
- •2.6 Приборы для измерения давления в жидкости
- •2.7 Сообщающиеся сосуды
- •2.8 Сила давления жидкости на плоские стенки
- •2.9 Закон Архимеда и его приложение
- •2.10. Поверхности равного давления
- •2.11 Сила давления жидкости на криволинейную стенку
- •Тема 3. Основы гидродинамики
- •3.1 Понятия и определения
- •3.1.1 Виды движения жидкости
- •3.1.2 Элементы потока жидкости.
- •3.1.3 Гидравлические параметры потока жидкости
- •3.2 Уравнение неразрывности или уравнение расхода
- •3.3 Режимы движения жидкости. Опыты Рейнольдса
- •3.4. Кавитация
- •3.5 Уравнение Бернулли для элементарной струйки идеальной жидкости
- •3.6. Уравнение Бернулли для реальной жидкости
- •3.7. Измерение скорости потока и расхода жидкости
- •3.8 Общие сведения о гидравлических сопротивлениях
- •Тема 4 Ламинарное течение жидкости в круглых трубах
- •4.1 Уравнение равномерного движения жидкости в круглой трубе
- •4.2. Расход, средняя скорость и потери напора при ламинарном течении жидкости в круглой трубе
- •Тема 5 Турбулентное течение жидкости в круглых трубах
- •5.1 Основные сведения
- •5.2 Распределение скоростей по живому сечению круглой трубы
- •5.3 Структура турбулентного потока жидкости в круглой трубе
- •5.4 Шероховатость стенок труб
- •5.5 Гидравлически гладкие и гидравлически
- •5.6 Потери напора по длине трубы
- •5.7 Опыты и. И. Никурадзе
- •Тема 6. Местные гидравлические сопротивления
- •Внезапное расширение русла.
- •Постепенное расширение русла.
- •6.3. Внезапное сужение русла.
- •Постепенное сужение русла.
- •Внезапный поворот трубы (колено).
- •6.6. Постепенный поворот трубы (закругленное колено или отвод).
- •6.7 Принцип сложения потерь напора.
- •6.8. Выражение полных потерь напора в виде степенной функции расхода
- •Тема 7 Истечение жидкости через отверстия и насадки
- •7.1 Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре
- •7.2. Истечение жидкости через насадки при постоянном напоре
- •7.3 Истечение жидкости через затопленное отверстие или насадок, или истечение под уровень
- •7.4 Применение отверстий и насадков
- •7.5 Истечение жидкости через отверстие или насадок при
- •7.6 Взаимодействие струи с твердой преградой
- •Тема 8 Гидравлический расчет трубопроводов
- •8.1 Классификация трубопроводов
- •8.2 Простой трубопровод постоянного сечения
- •8.3 Самотечный трубопровод
- •8.4 Сифонный трубопровод
- •8.5 Основы технико-экономического расчёта простых трубопроводов
- •8.6 Последовательное соединение трубопроводов
- •8.7 Параллельное соединение трубопроводов
- •8.8 Разветвленное соединение.
- •8.9. Сложные трубопроводы
- •8.10. Трубопроводы с насосной подачей жидкостей
- •8.11 Гидравлический удар в напорных трубопроводах
- •8.11.1 Явление гидравлического удара
- •8.11.2 Скорость распространения ударной волны
- •8.11.3 Определение повышения давления при гидравлическом ударе
- •8.11.4 Меры, предотвращающие возникновение гидравлического удара
- •8.11.5 Использование гидравлического удара
- •8.12 Равномерное движение жидкости в открытых руслах
- •8.13. Формулы для определения коэффициента Шези с
- •Библиографический список
2.4 Дифференциальные уравнения Эйлера равновесия жидкости
Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на нее действуют не только сила тяжести, но и другие массовые силы.
Рисунок 9 — К выводу дифференциальных уравнений Эйлера равновесия жидкости |
В покоящейся жидкости произвольно расположим прямоугольные оси координат. В пределах этих осей выделим элементарный параллелепипед с ребрами dx, dy, dz, параллельными осям координат (рисунок 7). Предположим, что жидкость в этом объеме затвердела. |
Тогда на гранях параллелепипеда действуют силы давления Р1, Р2, Р3, Р4, Р5, Р6, а в его центре тяжести приложена равнодействующая всех массовых сил Q.
Параллелепипед находится в равновесии. Напишем условие равновесия для оси х:
![]() (19)
(19)
Если принять, что р1 = р, то в связи с изменением координаты на величину dx
![]()
Проекция на ось х равнодействующей массовой силы Q найдётся из уравнения
![]()
где
![]() проекция ускорения массовой силы Q
на ось х.
проекция ускорения массовой силы Q
на ось х.
Подставляя
![]() и
и
![]() в уравнение (18) и сокращая на объём
dxdydz,
получим:
в уравнение (18) и сокращая на объём
dxdydz,
получим:![]()
или, разделив обе части последнего равенства на :
![]()
Проведя аналогичные рассуждения для условий равновесия относительно двух других осей, получим систему дифференциальных уравнений, носящих имя Эйлера:
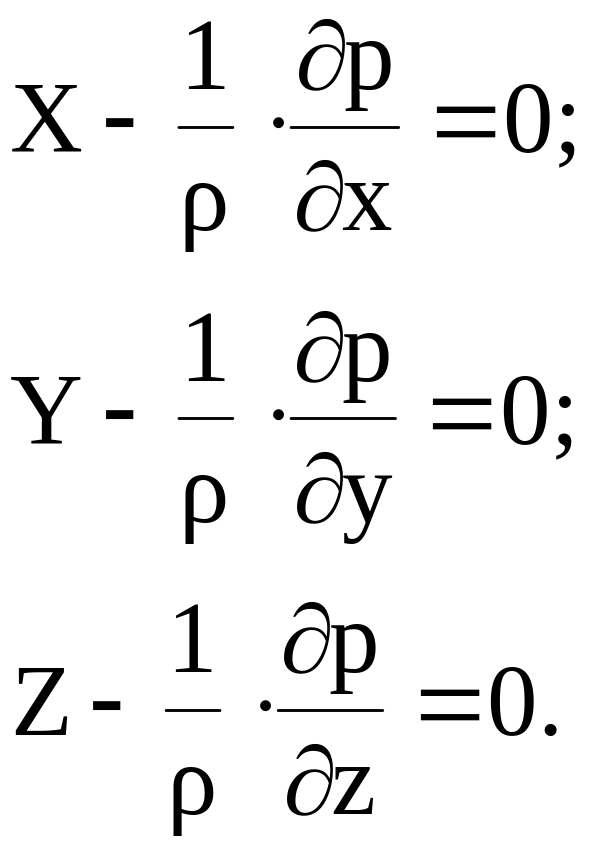 (20)
(20)
2.5 Абсолютное и избыточное давление. Вакуум
Давление на поверхности Земли, называемое атмосферным или барометрическим, постоянно изменяется в зависимости от метеоусловий. Зависит оно и от высоты расположения точки, в которой оно измеряется, над поверхностью Земли.
В технике считают, что:
![]()
Но в системе единиц СИ нет кгс, нет см2.
Известно, что 1 кгс = 9,81 Н; 1 см2 = 10-4 м2.
Тогда
![]()
Приняв за величину атмосферного давления величину
1 атм = 1 кгс/см2, мы за ноль отсчета приняли давление в абсолютной пустоте.
Так что на поверхности Земли Рабс = 1атм = 1 кгс/см2.
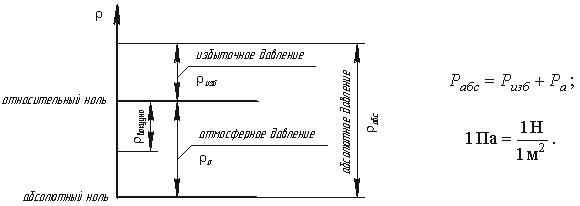
Давление, отсчитываемое от абсолютного нуля называется абсолютным (полным).
В технике чаще используют избыточное давление — это превышение абсолютного давления над атмосферным, или избыток давления над атмосферным.
Таким образом, связь между абсолютным и избыточным давлением:
Ризб = Рабс – Ратм. (21)
Рабс = Ратм + Ризб. (22)
Отрицательное избыточное давление называется вакуумом (разрежением), или вакуум — это недостаток давления до атмосферного.
Причём записи Ризб = - 0,72 атм и Рвак = 0,72 атм идентичны, это одно и тоже давление.
Пределы изменения вакуума: 0 Рвак 1 атм.
Максимальное значение вакуума: Рвак max = 1 атм.
Рис.10 Схема установки пьезометра
А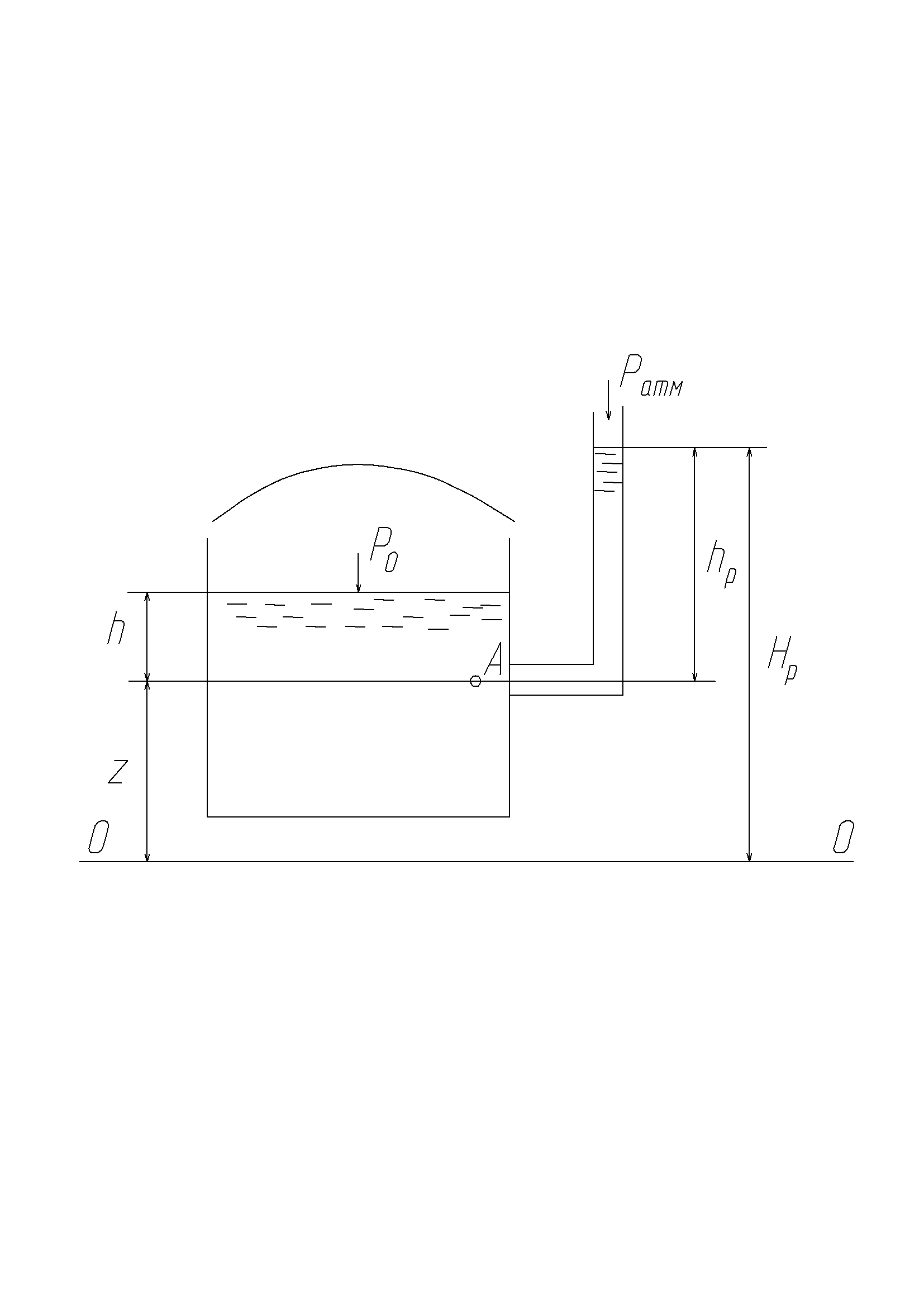 бсолютное,
или полное, гидростатическое давлении
состоит их внешнего давления на свободную
поверхность жидкости и манометрического
(избыточного)
даления, которое создает слой воды над
рассматриваемой точкой А.
бсолютное,
или полное, гидростатическое давлении
состоит их внешнего давления на свободную
поверхность жидкости и манометрического
(избыточного)
даления, которое создает слой воды над
рассматриваемой точкой А.
В открытом сосуде на свободную поверхность жидкости действует атмосферное давление. Обозначим его Ратм., а манометрическое (избыточное) Рман., тогда абсолютное давление Рабс = Ратм + Рман.. следовательно, основное уравнение гидростатики можно записать так:
Рабс = Ратм +h
Из рисунка 10 видно, что в закрытом сосуде Рабс = Ратм +hр, а с другой стороны Рабс = Р0+h, следовательно Ратм +hр=Р0+h, откуда можно записать:
![]()
Величина hр – пьезометрическая величина,показывающее избыточное давление в точке, где присоединена трубка (пьезометр). В открытом сосуде hр= h, так как Р0=Ратм, т.е. пьезометрическая высота будет равна глубине погружения точки А в жидкость. Высоту поднятия воды в пьезометре относительно плоскости отсчета 00 называют пьезометрическим напором Нр. Для закрытого сосуда:
![]()
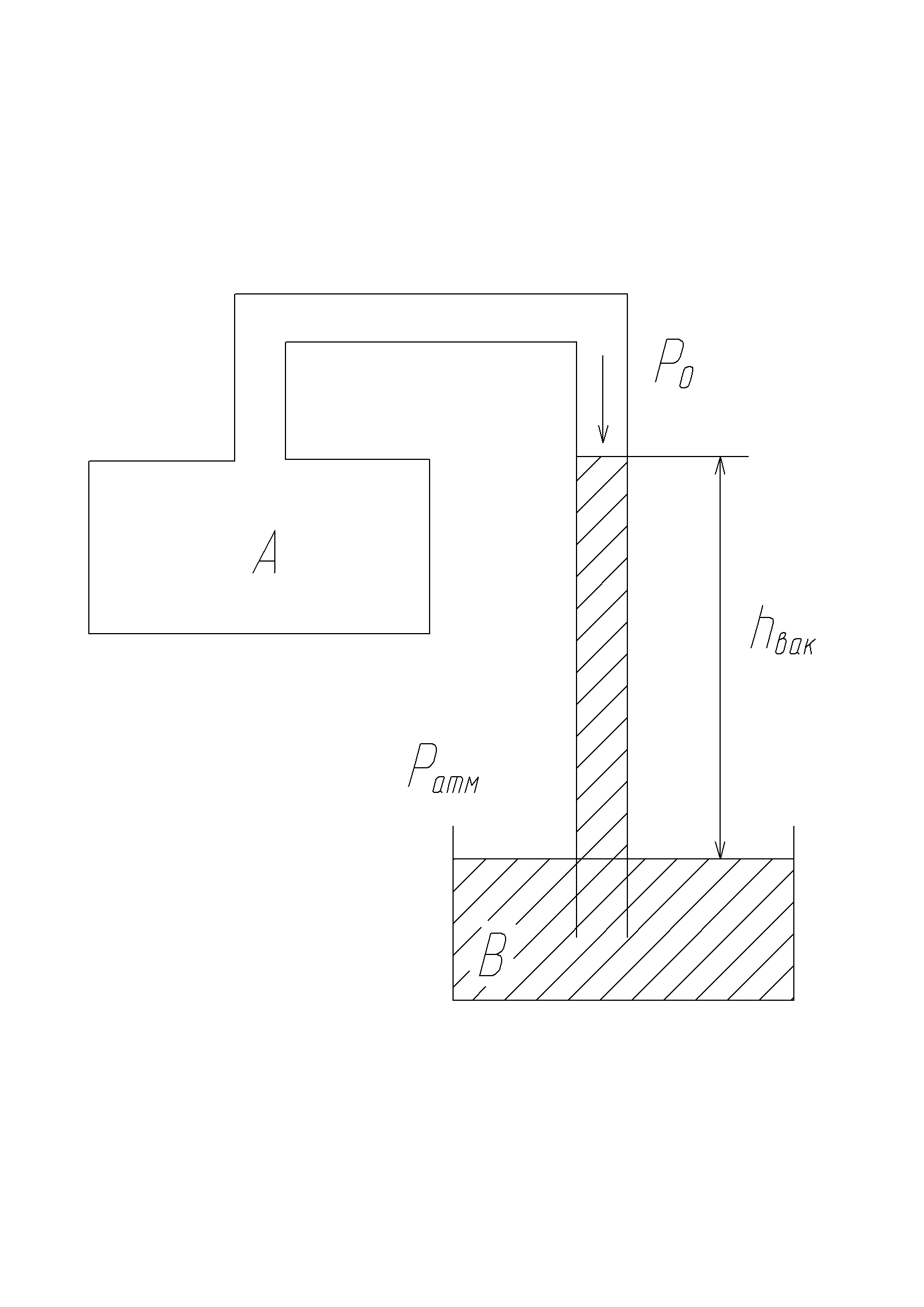
Для измерения вакуума используют вакуумметр. В связи с тем, что Р0<Ратм, жидкость поднимается в трубке из сосуда В на высоту hвак.
По уравнению Рабс = Ратм +h напишем:
Ратм = Р0 +hвак
Откуда
:
![]()
Задача: к котлу, заполненному водой, присоединена трубка, опущенная в стакан с ртутью. Определить Рабс и Ризб на дне котла.
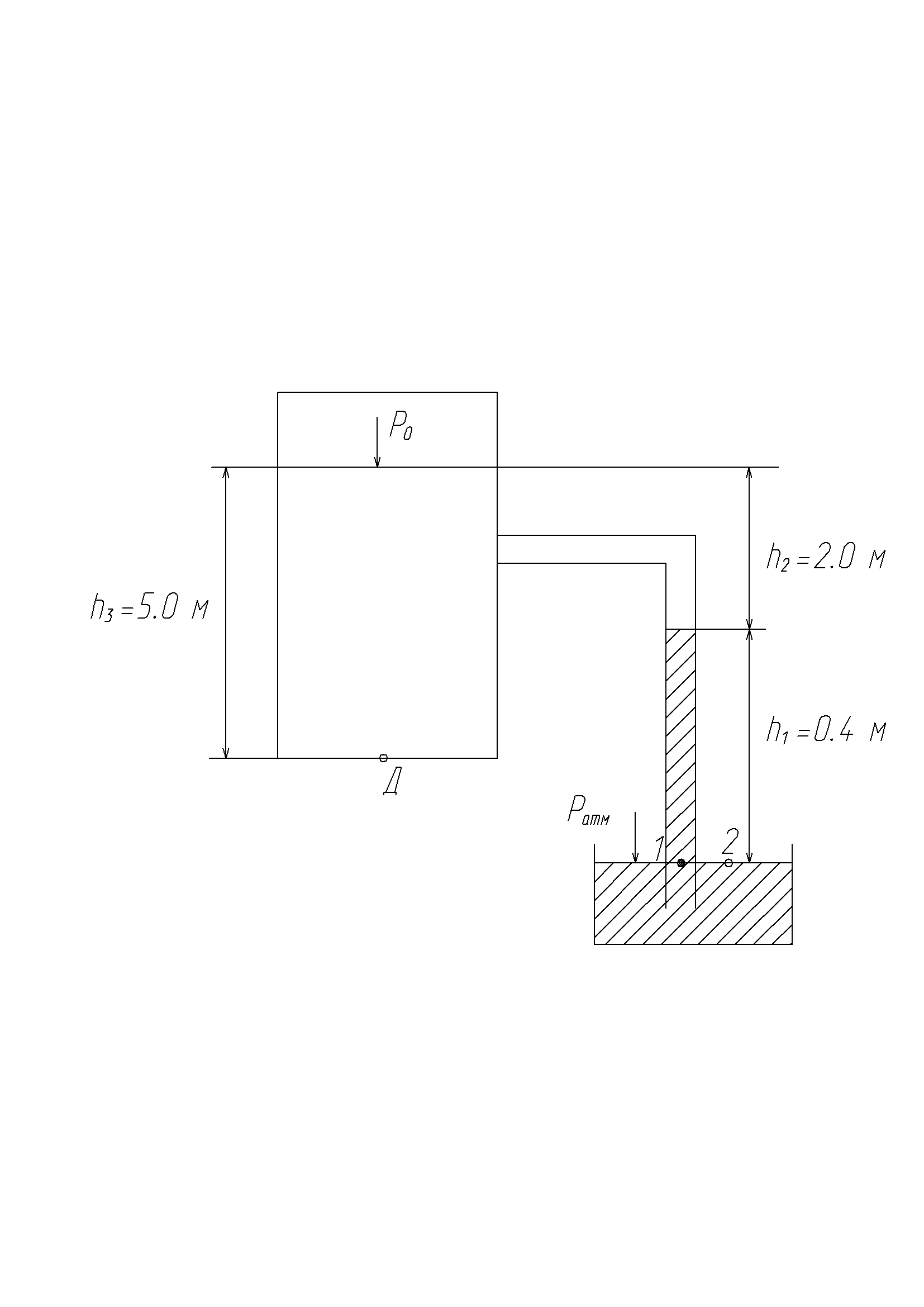
Решение: Р1 = Р2
Р1 = Р0 + ρвgh2 + ρртgh1
Р2 = Ратм;
Р0 = Ратм – g(ρвh2 + ρртh1) = 9.81*104 – 9.81(1000*2 + 13560*0.4) = 25270 Па
Рдабс = Р0 + ρвgh3 = 25270 + 1000*9,81*5 = 74320 Па
Рдизб = Рдабс - Ратм = 74320 – 9,81*104 = -23780 Па

