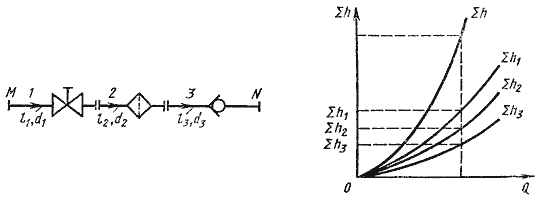
8.6 Последовательное соединение трубопроводов

Последовательное соединение трубопроводов — это соединение трубопроводов разного диаметра в одну нить (рисунок 73).

Рисунок 73 — Последовательное соединение трубопроводов

Имеется три последовательно соединённых трубопровода, длины которых диаметры d₁, d₂, d₃. На трубопроводах имеется ряд местных сопротивлений: задвижка, фильтр и обратный клапан.

Согласно уравнению расхода — расход вдоль потока остаётся постоянным:

(98)

Очевидно, что суммарные потери напора в последовательно соединённых трубопроводах:

(99)

Равенства (98) и (99) используются при расчётах последовательно соединённых трубопроводов.

Чтобы построить характеристику последовательно соединённых трубопроводов следует по формуле рассчитать характеристики каждого из трубопроводов, нанести их на график (рисунок 67), а затем на графике, взяв несколько разных расходов, при каждом из них сложить потери напора, получится суммарная характеристика последовательного соединения трубопроводов h_п. То есть следует сложить ординаты всех трёх кривых при разных абсциссах.

8.7 Параллельное соединение трубопроводов

Такое соединение нескольких простых трубопроводов, например, 1, 2 и 3 между точками M и N показано на рисунке (74). Параллельное соединение трубопроводов имеет две общие точки: M, в этой точке трубопроводы размыкаются и N, в этой точке трубопроводы соединяются вновь

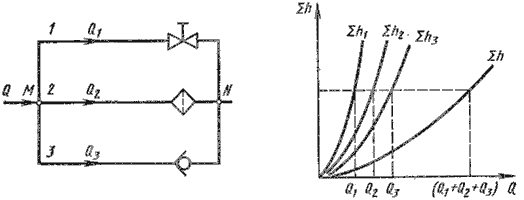
Рисунок 74 — Параллельное соединение

трубопроводов

Очевидно, что выполняется следующее равенство:

(100)

В точках M и N установлено по пьезометру. Так избыточное давление в точке M — Р_М, то жидкость в пьезометре, установленном в этой точке, под действием этого давления поднимется на высоту ; избыточное давление в точке N — Р_N, поэтому жидкость в пьезометре, установленном в этой точке, под действием этого давления поднимется на высоту

Потери напора в трубопроводах 1, 2 и 3 соответственно:

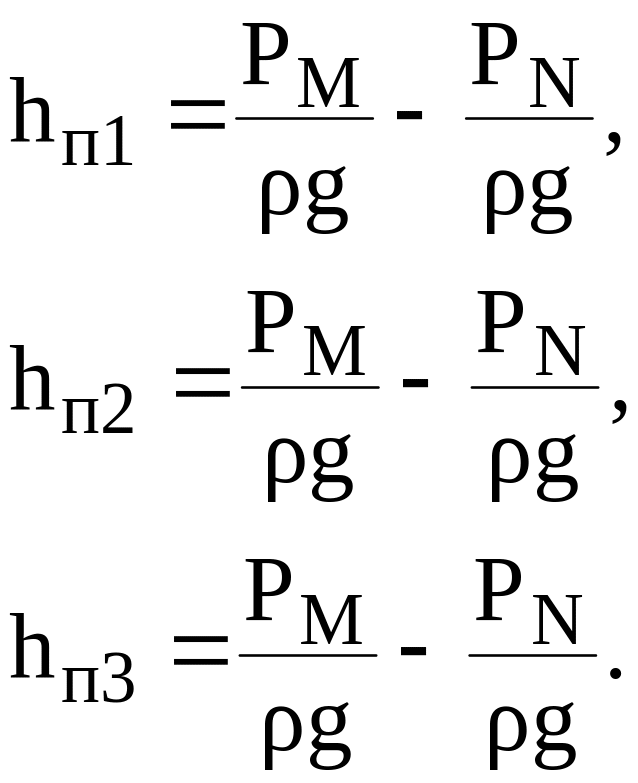(101)

Отсюда делаем следующий важный вывод:

(102)

то есть потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом

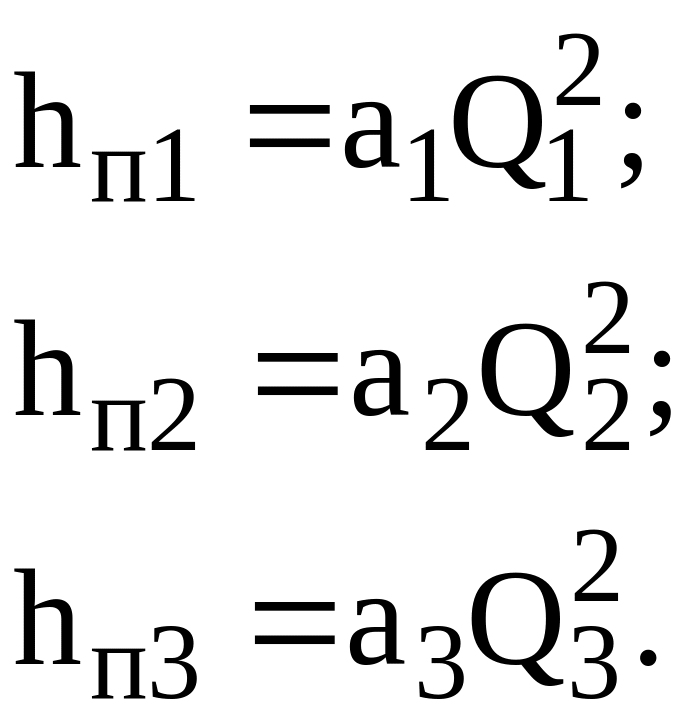(103)

Следовательно, в дополнение к уравнению (110) получаем на основании равенств (102), (103) ещё два уравнения:

(104)

То есть для параллельного соединения трубопроводов, состоящего из трёх ветвей, получили систему трёх уравнений (101), (104), из которой можно найти три неизвестных, например, расходы в параллельных ветвях Q₁, Q₂, Q₃, а затем и общий расход Q по уравнению (104).

Таким образом, для параллельного соединения трубопроводов, состоящего из n ветвей, составляется n уравнений, одно из которых для расходов, и n – 1 для потерь напора.

Из уравнений (100) и (104)вытекает следующее важное правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах (потерях напора).

Пример такого построения приведён на рисунке 74.