8.3 Самотечный трубопровод

Самотечный трубопровод — это такой простой трубопровод постоянного сечения, движение жидкости по которому происходит лишь за счёт разности высот начала и конца трубопровода (рис. 70).

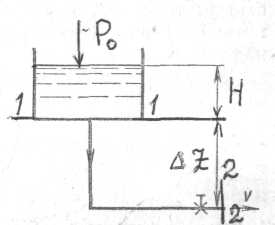
Рисунок 70 — Схема самотечного трубопровода

Для простого трубопровода постоянного сечения справедливо ранее полученное равенство (92):

(94)

В данном случае

Р₂ = Р_атм,

Тогда равенство (94) примет вид:

или после сокращения

(95)

по этому равенству рассчитывается самотечный трубопровод, оно показывает, что весь имеющийся напор идёт на преодоление гидравлических сопротивлений h_п.

Учитывая, что равенство (95) запишется:

откуда расход жидкости в самотечном трубопроводе:

где а — сопротивление трубопровода, рассчитывается по полученной выше по формуле:

8.4 Сифонный трубопровод

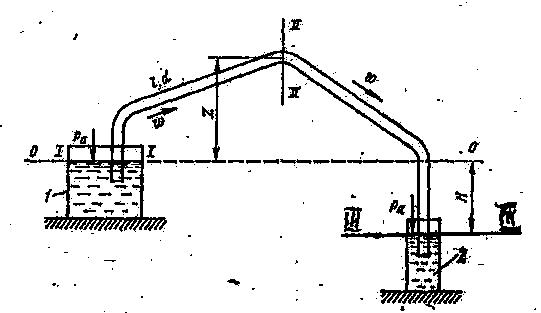
Сифонный трубопровод — это такой простой трубопровод постоянного сечения, часть которого расположена выше питающего его резервуара (рисунок 71).

Рисунок 71 — Схема к гидравлическому расчёту сифонного трубопровода

Для того чтобы сифонный трубопровод начал работать, необходимо его заполнить жидкостью, удалив воздух. Этого можно достигнуть путем повышения временно уровня резервуара (или давления в начале трубы) выше наивысшей точки сифона (уровня z) или путем отсасывания воздуха из сифона в наивысшей точке, благодаря чему под атмосферным давлением на уровнях I — I и II — II трубопровод заполнится жидкостью. Наконец, можно запереть концы сифона и залить его жидкостью через верхнюю точку, где одновременно выпускают заполнявший трубу воздух. После сплошного заполнения сифона жидкостью он начинает работать как обыкновенная труба. Расчетом обычно определяют пропускную способность сифона и предельное значение высоты z.

Так как сифонный трубопровод — это простой трубопровод постоянного сечения, то для него справедлива формула (93):

(96)

Проанализируем эту формулу для сечений I — I и III — III (плоскость сравнения проходит по сечению III — III):

Тогда формула (96) примет вид:

или после сокращений

откуда найдётся расход Q по сифонному трубопроводу:

где а — сопротивление трубопровода, рассчитывается по полученной выше по формуле:

Для определения высоты z, на которую может подняться жидкость в сифонном трубопроводе, составим уравнение Бернулли для сечений I — I и II — II:

(97)

Если плоскость сравнения 0 — 0, совпадает с поверхностью жидкости в резервуаре 1, то z₁ = 0; Р₁ = Р_а; ₁  0; _I = _II = 1 (принимаем режим движения жидкости турбулентным); z_II = z; р_II > p_н.п. — давление в сечении II — II должно быть больше давления насыщенных паров жидкости p_н.п. — давления, при котором жидкость закипает при данной температуре, иначе наблюдается явление кавитации — самовскипания жидкости в замкнутом объёме и образующиеся при этом пузырьки пара приводят к срыву работы сифонного трубопровода.

Тогда уравнение (97) примет вид:

откуда высота z, на которую может подняться жидкость в сифонном трубопроводе:

Например, для воды: Р_а = 10 м вод. ст. тогда:

Таким образом, максимальная высота, на которую может подняться жидкость в сифонном трубопроводе, перекачивающим воду, не превышает 10 м.

Задача. По сифонному трубопроводу длиной , диаметром d = 100 мм, К_Э = 0,3 мм,  = 4 переливается вода при t = 20⁰С с расходом Q = 20 л/с. Определить высоту z, на которую может подняться вода в сифонном трубопроводе.

Решение. Высота z найдётся по формуле:

Давление насыщенных паров воды при t = 20⁰С — 0,24 м вод. ст. [Справочник по гидравлическим расчетам / Под ред. П. Г. Киселева, стр.279].

Определяем скорость воды

Число Рейнольдса

режим турбулентный.

Предельные числа Рейнольдса:

— первое

— второе

Так как то зона сопротивления квадратичная, и коэффициент гидравлического трения  определяется по формуле Шифринсона:

Тогда высота, на которую может подняться вода в сифонном трубопроводе