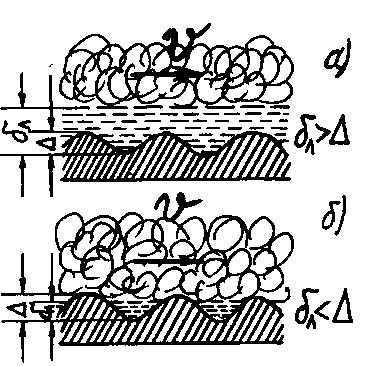
5.5 Гидравлически гладкие и гидравлически

шероховатые трубы

Рисунок 47 — Гидравлически гладкие и гидравлически шероховатые трубы

Пусть выступы шероховатости (рисунок 47 а) будут меньше, чем толщина ламинарного подслоя, то есть . Такие трубы называются гидравлически гладкими. При этом неровности стенки полностью погружены в этот подслой, турбулентная часть потока не входит в непосредственное соприкосновение со стенками и движение жидкости, а следовательно, и потери энергии не будут зависеть от шероховатости стенок, а будут обусловливаться лишь свойствами самой жидкости.

Если (рисунок 47, б) высота выступов такова, что они превышают толщину ламинарного подслоя, то есть то такие трубы называют гидравлически шероховатыми. Неровности стенок в таких трубах будут выступать в турбулентную область, увеличивать беспорядочность движения и существенно влиять на потерю энергии. Однако такое деление труб на гидравлически гладкие и гидравлически шероховатые условно. Так как толщина ламинарного подслоя не постоянна, она зависит от скорости потока жидкости (формула 57), она уменьшается с увеличением скорости и увеличивается, если скорость уменьшается.

Следовательно, одна и та же труба в зависимости от скорости  может вести себя по-разному: в одном случае — как гидравлически гладкая, а в другом — как гидравлически шероховатая.

5.6 Потери напора по длине трубы

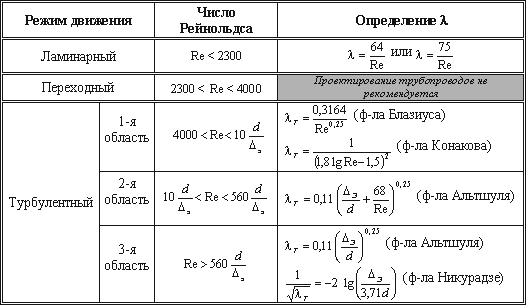
При турбулентном режиме, как и при ламинарном, потери напора по длине определяются по формуле Дарси-Вейсбаха:

(58)

Вся сложность заключается в определении коэффициента гидравлического трения .

Существует четыре зоны сопротивления (рисунок 48), в каждой из которых  определяется по своей формуле.

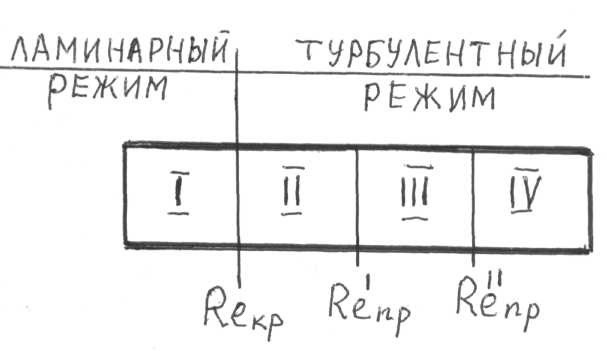
Рис.48 — Зоны сопротивления

Для определения коэффициента гидравлического трения  находят режим движения жидкости по числу Рейнольдса:

или

Если Re  Re_КР = 2320 режим движения жидкости ламинарный, и  определяется по формуле Дарси

. (59)

Если Re > Re_КР = 2320 режим движения жидкости турбулентный. При турбулентном режиме границами зон сопротивления являются предельные числа Рейнольдса:

— первое (60)

— второе (61)

Если окажется, что это зона гидравлически гладких труб, тогда  определяется по формуле Блазиуса

(62)

Если окажется, что это переходная зона сопротивления, тогда  определяется по формуле Альтшуля

(63)

Если окажется, что это квадратичная зона сопротивления, тогда  определяется по формуле Шифринсона

(64)

5.7 Опыты и. И. Никурадзе

И. И. Никурадзе испытал на сопротивление ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путем приклейки песчинок определенного размера, полученного просеиванием песка через специальные сита. Тем самым была получена равномерно распределенная зернистая шероховатость. Испытания были проведены при широком диапазоне относительных шероховатостей а также чисел Re (Re = 500  10⁶). Результаты этих испытаний представлены на рисунке 49, где построены кривые зависимости lg 100 от lg Re для ряда значений /d.

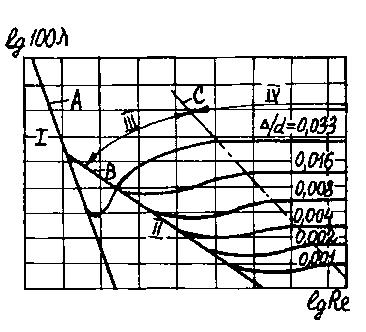
Рисунок 49 — Зависимость от для труб

с искусственной шероховатостью

Каждая кривая на графике представляет собой геометрическое место точек для труб с определённой относительной шероховатостью /d.

На графике (рисунок 49) можно выделить четыре зоны: I, II, III, IV.

Зона I — здесь для всех значений /d опытные точки легли на прямую А, то есть  = f(Re) и   f(/d), как и в формуле Дарси это зона ламинарного режима.

Зона II — здесь все опытные точки легли на прямую В, то есть  = f(Re) и   f(/d), как и в формуле Блазиуса это зона гидравлически гладких труб.

Зона III — между прямыми В и С, здесь как и в формуле Альтшуля

Зона IV — правее прямой С, здесь   f(Re), а  = f(/d), как и в формуле Шифринсона

Таким образом, И. И. Никурадзе своими опытами доказал справедливость формул для расчёта коэффициента гидравлического трения , предложенных другими исследователями.

Таблица 3

Таблица для определения коэффициента гидравлического трения