Тема 4 Ламинарное течение жидкости в круглых трубах

Как указывалось выше, ламинарное течение жидкости является строго упорядоченным, слоистым течением без перемешивания жидкости. Теория ламинарного течения жидкости основывается на законе жидкостного трения Ньютона. Это трение между слоями движущейся жидкости является единственным источником потерь энергии в данном случае.

4.1 Уравнение равномерного движения жидкости в круглой трубе

В потоке жидкости (рисунок 39), движущейся равномерно ( = const), между сечениями I и II выделим цилиндрический столбик жидкости с малым поперечным сечением S, со стенками, параллельными направлению движения. Составим уравнение Бернулли для сечений I и II:

(46)

Рисунок 39 — Силы, действующие при равномерном движении жидкости в круглой трубе

Так как скорости в сечениях I и II одинаковые: ₁= ₂, то равенство (42):

(47)

На выделенный цилиндрический столбик в направлении движения действуют следующие силы:

- сила давления

— сила трения (где  — периметр сечения цилиндра);

— проекция силы тяжести

При равномерном движении эти силы должны находиться в равновесии:

(48)

Заметив, что равенство (44) напишем:

Разделим последнее равенство на

(49)

В равенствах (47) и (49) левые части равны, значит, равны и правые:

(50)

Разделим последнее равенство на и учтём, что:

гидравлический радиус;

гидравлический уклон.

Тогда

(51)

то есть касательное напряжение при равномерном движении жидкости в круглой трубе равно:

(52)

Равенство (52) — уравнение равномерного движения жидкости в круглой трубе.

4.2. Расход, средняя скорость и потери напора при ламинарном течении жидкости в круглой трубе

Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу (рис.40).

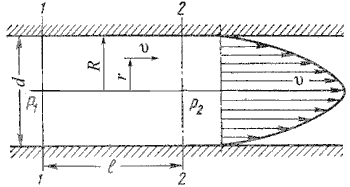
Рис. 40. Схема для рассмотрения ламинарного потока

Уравнение, связывающее переменные υ и r, имеет следующий вид:

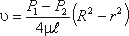
где P1 и P2 - давления соответственно в сечениях 1 и 2.

У стенок трубы величина r = R, значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной

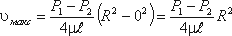
Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.

Максимальная скорость дает высоту параболоида

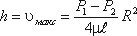
Как известно из геометрии, объем параболоида высотой h и площадью ρR² равен

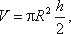
а в нашем случае

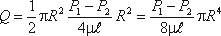
Если вместо R подставить диаметр трубы d, то формула приобретет вид

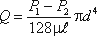
Расход в трубе можно выразить через среднюю скорость:

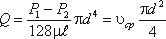(53)

откуда

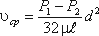
Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.40).

Потеря давления в трубопроводе будет равна:

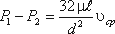
Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:

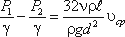
Так как левая часть полученного равенства равна потерям напора h_пот в трубе постоянного диаметра, то окончательно это равенство примет вид:

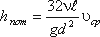(54)

Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:

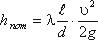(55)

где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:

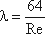
Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re < 2300 применять формулу

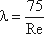
Формулу (49) можно также использовать при расчете трубопроводов и открытых русел с любой формой живого сечения потока, если заменить в ней диаметр гидравлическим радиусом.

(56)

Задача: По трубе длиной l=100 м; d=100 мм; перекачивается 10 л/с жидкости. Определить потери напора по длине, если =0,726 см²/с.

Решение:

- ламинарный режим

м.