3.7. Измерение скорости потока и расхода жидкости

Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.38), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

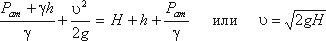
где Н - столб жидкости в трубке Пито.

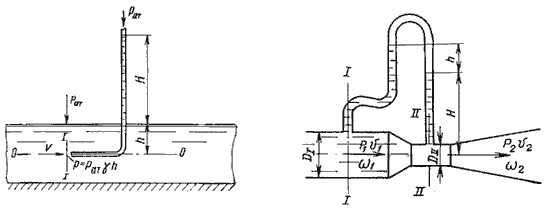
Рис. 38. Трубка Пито и pасходомер Вентури

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.38). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z₁ = z₂ , напишем уравнение Бернулли для сечений I-I и II-II:

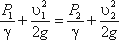
или

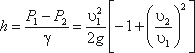
Используя уравнение неразрывности

Q = υ₁S₁ = υ₂S₂

сделаем замену в получено выражении:

Решая относительно Q, получим

Выражение, стоящее перед , является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

3.8 Общие сведения о гидравлических сопротивлениях

Силы, препятствующие движению жидкости, называются гидравлическими сопротивлениями.

При движении потока реальной жидкости происходят потери напора, так как часть удельной энергии потока затрачивается на преодоление различных гидравлических сопротивлений. Количественное определение потерь напора Н_пот является одной из самых важнейших задач гидродинамики, без решения которой невозможно практическое использование уравнения Бернулли.

Гидравлические сопротивления бывают двух видов:

— линейные гидравлические сопротивления.

— местные гидравлические сопротивления; в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.

Для определения потерь напора по длине потока Н_дл в круглой цилиндрической трубе применяется формула Дарси-Вейсбаха:

(41)

где  - коэффициент Дарси, характеризующий сопротивление по длине трубопровода;

l – длина трубы;

 - средняя скорость потока;

d – внутренний диаметр трубы;

g – ускорение свободного падения.

Эту формулу можно также использовать при расчете трубопроводов и открытых русел с любой формой живого сечения потока, если заменить в ней диаметр гидравлическим радиусом:

Кроме формулы Дарси-Вейсбаха в гидравлике широко применяется

(42)

представляющая собой несколько иную форму выражения той же зависимости. Действительно, учитывая, что:

(43)

и решая относительно Н_дл, получим:

, (44)

где - коэффициент Шези, единица которого в системе СИ -

для определения коэффициентов  и С существует много формул различных авторов. О некоторых из этих формул, имеющих применение в настоящее время, будет сказано ниже при рассмотрении закономерностей ламинарного и турбулентного режимов движения жидкости.

Определение потерь напора в местных сопротивлениях Н_м производится по формуле Вейсбаха:

(45)

где  - коэффициент местного сопротивления, который для различных местных сопротивлений находится опытным путем, а при расчетах принимается из справочников.

Общие потери напора в трубопроводе или открытом русле определяются путем арифметического суммирования потерь напора на прямолинейных участках и в местных сопротивлениях, т.е.

Этот метод носит название принципа наложения (сложения) потерь.