План Лекция 5
Краткая историческая справка.
Новые задачи российской математики в середине XVIII века.
Развитие основных понятий математического анализа в работах Эйлера.
Систематизация Эйлером дифференциального и интегрального исчисления.
Развитие теории дифференциальных уравнений.
Исследования Эйлера по вариационному исчислению.
Работы Эйлера по геометрии.
Теоретико-числовые мемуары Эйлера.
Элементы теории вероятностей в исследованиях Эйлера.
Краткая историческая справка
Экономические темпы развития к 1750 г. в России замедлились, сказывалась продолжительная Северная война (1700-1721 гг.) между Швецией и Северным союзом (Россия, Саксония, Польша, Дания) за гегемонию на Балтике и частые дворцовые перевороты.
Культура России развивалась по пути, намеченному в начале века. Из всех школ дальнейшее развитие получили только профессиональные школы, готовившие, в основном, военные кадры. В 1731 году был открыт Сухопутный шляхетский корпус, Морская академия была преобразована в Морской шляхетский кадетский корпус, Артиллерийская и Инженерная школы объединены в Артиллерийский и инженерный шляхетский корпус. Из начальных школ сохранились лишь гарнизонные для солдатских детей, школы при горных заводах, при московском госпитале и кое-где – цифирные школы.
В 40-х годах благодаря усилиям М.В. Ломоносова и других русских учёных оживилась учебная жизнь в гимназии и университете ПАН. Петербургская академия наук стала центром научной жизни страны. Уже в 1736 г. известный французский физик Дорту де Меран писал:
«Петербургская академия со времени своего рождения поднялась на выдающуюся высоту науки, до которой академии Парижская и Лондонская добрались только за 60 лет упорного труда».
Научная, просветительская и организаторская деятельность Михаила Васильевича Ломоносова составила целую эпоху в истории Академии и российской науки. Он обогатил её фундаментальными открытиями в химии, физике, астрономии, геологии, географии; внес большой вклад в разработку истории, языкознания и поэтики; организовал в 1748 г. первую химическую лабораторию; активно участвовал в 1755 г. в основании Московского университета, ныне носящего его имя.
Первый принцип ПАН, стимулирующий развитие русской науки, была обязательная связь исследований с практическими потребностями страны.
По инициативе Академии были:
проведены экспедиционные исследования, внесшие огромный вклад в раскрытие природных ресурсов России,
проведены этнографические исследования территорий страны от Белого до Каспийского морей, от западных областей до Камчатки,
составлены карты обследованных районов с указанием полезных ископаемых,
изучен их животный и растительный мир,
описаны история, этнография, хозяйственная деятельность живущих там народов и начато изучение их языков.
Медленно, но неуклонно происходила русификация Академии. В 1746 году появился первый русский президент - граф К. Г. Разумовский, начали избираться отечественные ученые. (С. П. Крашенинников, М. В. Ломоносов, поэт В. К. Тредиаковский, а позже астрономы Н. И. Попов, С. Я. Румовский, П. Б. Иноходцев, натуралисты И. И. Лепехин, Н. Я. Озерецковский, В. Ф. Зуев и др.).
Новые задачи российской математики в середине XVIII века
Дальнейший технический прогресс в XVIII веке был невозможен без развития всего естествознания, и без развития математических методов. О новых задачах и проблемах математики можно судить по состоянию важнейших областей естествознания в данное время:
основы общей механики были заложены И. Ньютоном в «Началах натуральной
философии», но
основные достижения относились лишь к механике точки,
в механике твёрдого тела рассмотрено только вращение вокруг неподвижной оси,
исследованы только простейшие случаи движения тела в неподвижной среде.
Ньютоном и Лейбницем было открыто исчисление бесконечно малых, но
новые методы только завоёвывали призвание,
существовали споры по обоснованию исчисления,
в математических работах Ньютона приведены методы интегрирования ДУ, но в работах по механике Ньютон часто отказывался от новых методов.
→ Таким образом, у математики и механики появилась задача создания аналитических методов (основная роль в её решении принадлежит Л. Эйлеру).
В связи с созданием аналитической механики возникли новые задачи для математического анализа:
необходим был аппарат для развития теорий малых колебаний материальной точки и систем точек,
необходима разработка теории физического маятника для исследований по гравитометрии, теории движения планет, нужд мореплавания и геодезии
Кеплером и Ньютоном установлены законы невозмущённого движения планет, к середине XVIII века они были достаточно для практики изучены с помощью геометрических методов, недостаточными для изучения более сложных законов. Поэтому необходимо было разработать новые аналитические методы в динамике:
Астрономические наблюдения показали, что Сатурн и Юпитер не подчиняются кеплеровским законам движения планет. Поэтому возникла задача объяснения этих возмущений теоретическими методами.
Несмотря на открытия Ньютона, теория Луны находилась в неудовлетворительном состоянии: знание точного положения Луны позволяло достигать более точного определения времени и долгот. В 1750 г. был объявлен конкурс математического объяснения возмущений в движении Луны (Клеро, Лаплас). Решение этой задачи привело к классической задаче трёх тел.
Принципиальные трудности, возникающие при решении системы ДУ, описывающих взаимодействие 3 тел, настолько велики, что в самом общем виде задачу нельзя считать решённой и в наши дни.
Исследование проблемы о взаимосвязи между движением и формой небесных тел привело к созданию теории потенциала (задача поставлена Эйлером).
В решении проблемы о вращении Земли начальные результаты принадлежат Эйлеру и Даламберу, причём Эйлеру принадлежат динамические уравнения, определяющие это движение – нелинейная система трёх ДУ 2-го порядка относительно эйлеровых углов
,
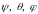как функций времени.
→ Таким образом, возникла вторая крупная задача для математического анализа – построение теории ДУ в частных производных.
Проблема звучащей струны имела значение для развития всего математического анализа не только в XVIII, но и в XIX вв. Длительный спор о характере допустимых функций, входящих в решение уравнения колебания струны, (Даламбер, Эйлер, Д. Бернулли, Лагранж) привёл к развитию понятия функции.
Задачи гидродинамики, сложившейся к середине XVIII века, также требовали создания аналитических методов - теоретических методов гидродинамики (решение – в работах Д. Бернулли, Даламбера, Эйлера и Лагранжа).
Интерес к математическому анализу усилился постановкой ряда новых геометрических задач в ходе развития дифференциальной геометрии.
→ Таким образом, в теории ДУ накопилось много частных результатов, которые необходимо было систематизировать.