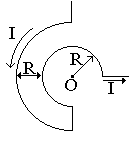4.3 Задание для самостоятельного выполнения по вариантам

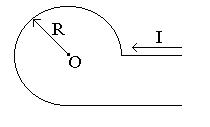
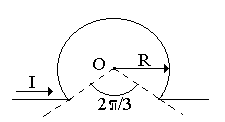
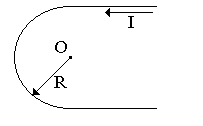
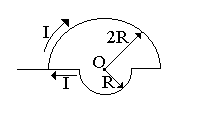
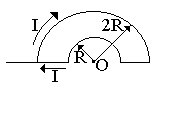
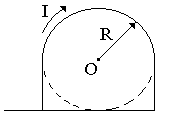
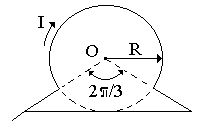
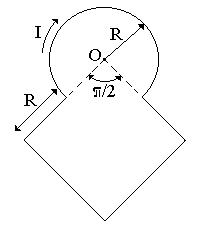
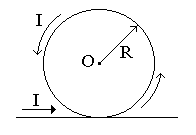
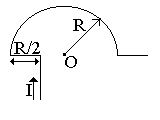
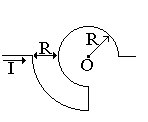
Бесконечно длинный тонкий проводник с током I = 100 А изогнут так, как показано на рисунке 4.3. Радиус изгиба R = 10 см. Определить в точке О магнитную индукцию поля В, создаваемого этим током. Направление тока показано на рисунке стрелкой.

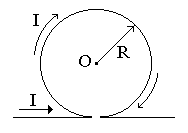
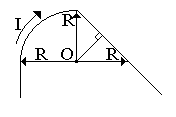
вариант 1	вариант 2	вариант 3
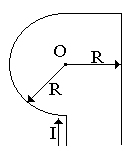
вариант 4	вариант 5	вариант 6

Рисунок 4.2

вариант 7		вариант 8			вариант 9
вариант 10			вариант 11			вариант 12
вариант 13	вариант14			вариант 15			вариант 16

Продолжение рисунка 4.3

5 Тема 4: Сила, действующая на заряд, движущийся в магнитном поле

5.1 Основные формулы и указания к решению задачи

Сила, действующая на провод с током в магнитном поле (закон Ампера),

или , (5.1)

где l – длина провода,  – угол между направлением тока в проводе и вектором магнитной индукции .

Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в отдельности:

. (5.2)

Сила Лоренца – или , (5.3)

где – скорость заряженной частицы, – угол между векторами и .

Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора  (если заряд положительный), то отогнутый большой палец покажет направление силы Лоренца.

Отметим, что магнитное поле действует только на движущиеся в нем заряды, на покоящиеся электрические заряды магнитное поле не действует.

5.2 Пример решения задачи

Рассмотрев фотографию треков заряженных частиц, двигавшихся в магнитном поле определить отношение заряда к массе неизвестной частицы, а также знак заряда этой частицы, если известно, что левый трек принадлежит ядру атома водорода, правый неизвестной частице. Отношение заряда атома водорода к его массе равно 9,610⁷ Кл/кг. Модули начальных скоростей частиц одинаковы. Индукция магнитного поля 2,2 Тл. Направление магнитного поля показано на рисунке 5.1.

Решение: Для решения этой задачи оба трека осторожно переносят на кальку или делают ксерокопию рисунка. Затем измеряют радиусы кривизны треков. Для этого вначале находят центры кривизны. В средних участках треков проводят по две хорды и в середине к ним восстанавливают перпендикуляры. Точки пересечения перпендикуляров будут центрами кривизны треков. Затем измеряют радиусы кривизны с помощью измерительной линейки, учитывая масштаб снимка.

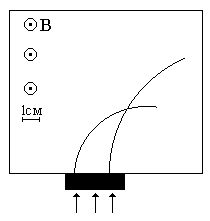
Рисунок 5.1

Для нашего случая R₁ = 0,032 м, R₂ = 0,072 м.

На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, вектор которой перпендикулярен вектору скорости частицы. Эта сила является центростремительной силой:

F_л = qB, , F_л = F_ц.с. , (5.4)

. (5.5)

Отсюда модуль скорости неизвестной частицы ₁ будет равен:

, (5.6)

где q₁ – заряд частицы, m₁ – масса частицы, R₁ – радиус кривизны трека, B – модуль магнитной индукции.

Модуль скорости ядра атома водорода ₂ равен:

, (5.7)

где q₂ – заряд ядра водорода, m₂ – масса ядра атома водорода, R₂ – радиус кривизны трека.

Так как по условию ₁ = ₂, то

. (5.8)

Отсюда получаем:

. (5.9)

Подставляя в последнюю формулу числовые данные, получаем:

Кл/кг.

Выполним проверку единиц измерения величин.

. (5.10)

Воспользовавшись правилом левой руки определяем, что наша частица заряжена положительно.