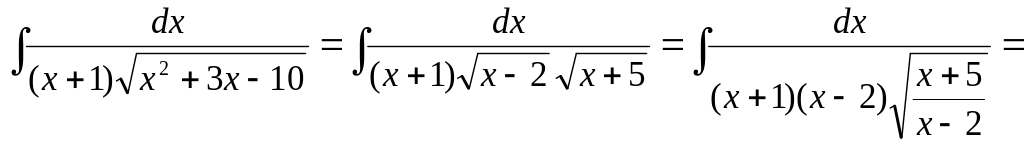2.1.4. Інтегрування раціональних функцій

Тригонометричним інтегралом називають . З того, що та даний інтеграл можна звести до

Теорема. Будь-який тригонометричний інтеграл раціоналізується за допомогою так званої універсальної підстановки

(-  х )

Універсальну підстановку слід застосовувати у випадках

, ,

Приклад 15. Знайти інтеграл

Розв’язання.

Але іноді зручно застосовувати частинні підстановки, а саме:

1. R(-sinx, cosx) = - R(sinx, cosx)

Якщо при заміні sinx на – sinx вираз R(sinx, cosx) змінює знак, то застосовують підстановку cosx=t

Приклад 16. Знайти інтеграл

Розв’язання.

2. R(sinx,- cosx) = - R(sinx, cosx)

Якщо при заміні cosx на –cosx вираз R(sinx, cosx) змінює знак, то застосовують підстановку sinx = t

3. R(-sinx,- cosx) = R(sinx, cosx)

Якщо при заміні cosx на –cosx та sinx на – sinx функція R(sinx, cosx) не змінює знак, то застосовують підстановку tgx = t або ctgx = t

Приклад 17. Знайти інтеграл.

Розв’язання.

.

2.1.6. Інтегрування гіперболічних функцій

1) ;

2) ;

3) ;

4)

Будь-який гіперболічний інтеграл раціоналізується за допомогою підстановки e^x=t (e^x 0), .

Оскільки та , то після підстановки отримаємо інтеграл від раціональних функцій .

Часто має сенс застосування певних співвідношень:

Приклад 17. Знайти інтеграл.

Розв’язання.

2.1.7. Інтегрування ірраціональних функцій

Будь-який інтеграл такого виду раціоналізується за допомогою підстановки , до інтеграла такого виду приводять також інтеграли . В цьому випадку m спільне кратне знаменників дробів тоді звідси , тобто підінтегральна функція є раціональною функцією від х та

Приклад 18. Знайти інтеграл

Розв’язання.

Диференціальним біномом інтеграла називається підінтегральний вираз, де a і b – довільні сталі, m, n, p – раціональні числа Інтеграл від диференціального бінома обчислюється в скінченому вигляді тільки в таких трьох випадках:

1) p  Ζ. Підстановка: х=t^k , k – спільний знаменник чисел m і n;

2) . Підстановка: , k –знаменник числа p;

3) . Підстановка: , k –знаменник числа p.

Якщо жодна з цих умов не виконується, то диференціальний біном не інтегрується в елементарних функціях (теорема Чебишев).

Приклад 19. Знайти інтеграл

Розв’язання. , отже →

Інтеграл , де R – раціональна функція від і від х. Розглянемо інтеграл у випадку коли квадратний тричлен не має однакових коренів, тоді раціоналізують такий інтеграл за допомогою підстановок Ейлера.

І підстановка Ейлера. Якщо а, то

Приклад 20. Знайти інтеграл

Розв’язання. ,

ІІ підстановка Ейлера. Якщо с 0, то

ІІІ підстановка Ейлера. Якщо має різні дійсні корені (, ), вважаючи х : , то інтеграл раціоналізується підстановкою

Приклад 21. Знайти інтеграл

Розв’язання.