1.5. Схема дослідження функції.

1. Знайти область визначення, область значення функції;

2. дослідити функцію на парність та непарність, періодичність;

3. знайти точки перетину графіка функції з осями системи координат, точки розриву, проміжки знакосталості функції;

4. знайти нулі та точки розриву похідної, інтервали монотонності функції, точки екстремуму та екстремальні значення функції;

5. знайти нулі та точки розриву другої похідної, інтервали опуклості графіка функції, точки перегину та значення функції в цих точках;

6. дослідити поводження функції біля точок розриву та на нескінченості, знайти, якщо вони є асимптоти графіка

Приклад 14. Провести повне дослідження функції та побудувати її графік.

Розв’язання.

1) Знайдемо область визначення функції. Необхідно знайти ті точки, в яких знаменник дробу дорівнює нулю і виключити їх. Одержимо . Функція визначена в інтервалах .

2) Функція непарна. Тому її графік симетричний відносно початку координат. Функція не є періодичною. Це випливає навіть з того, що вона невизначена лише у двох точках.

3) Знайдемо точки перетину графіка функції з осями координат: при х=0, у=0, при у=0, х=0. Інших точок не існує.

4) Дослідимо функцію на монотонність та критичні точки. Для цього знайдемо першу похідну функції. Маємо:

;

.

Тоді для всіх із області неперервності.

Тобто функція спадна на кожному інтервалі області визначення.

5) Дослідимо функцію на опуклість та точки перегину. Для цього знайдемо другу похідну.

Прирівняємо . Одержимо ;

х=0 – критична точка.

Знайдемо знак другої похідної в кожному з інтервалів . На проміжках (-;-5), (0;5) у ^//(x)<0 – графік функції опуклий вгору; на проміжках (-5;0), (5;+ ) у ^//(x)>0 – графік функції опуклий вниз. Точка є точкою перегину графіка функції.

6) Знайдемо асимптоти графіка функції.

а) Вертикальні асимптоти будемо шукати в точках розриву функції. Одержимо

Прямі та є вертикальними асимптотами функції.

б) Похилі асимптоти будемо шукати у вигляді , а невідомі параметри і визначимо за формулами . Одержимо

, тоді – вісь – похила асимптота.

Рис. 8

П

Рис. 8

риклад 15. Провести повне дослідження функції та побудувати графік

Розв’язання.

1) Область визначення функції у(х): (-;0)(0;+).

2) Функція парна, бо .

3) Функція не є періодичною. Це випливає навіть з того, що вона має лише один нуль, або з того, що функція невизначена лише в одній точці.

4) Дослідимо функцію на монотонність і критичні точки. Знайдемо похідну:

. Критичні точки х₁=1, х₂=-1.

На проміжках (-;-1), (0;1) у ^/(х)<0, тому на цих проміжках функція спадає. На проміжках (-1;0), (1;+) у ^/(х)>0, тому на цих проміжках функція зростає.

Оскільки при переході через точки х₁=1, х₂=-1 похідна змінює знак з мінуса на плюс, то в цих точках маємо локальний мінімум, який дорівнює

5) Дослідимо функцію на опуклість та точки перегину. Знайдемо другу похідну

Звідси випливає, що у ^//(х)>0 для х(-;0)(0;+).Отже, на обох проміжках графік функції опуклий вниз. Точки перегину відсутні.

6) Застосувавши правило Лопіталя, знайдемо границю функції в точці 0:

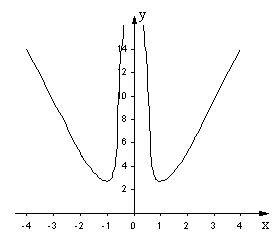
Отже, вісь ординат служить для графіка функції вертикальною асимптотою. Знайдемо границю функції на нескінченості: . Таким чином, множиною значень функції є проміжок [e;+)