2.2.1. Невласні інтеграли

Нехай функція f(x) визначена на відрізку [a;b] за винятком, можливо, скінченої множини точок {x_k}цього відрізка. Тоді якщо f(x) необмежена на відрізку [a;b], який не містить точок x_k, то вираз називають невласним інтегралом від необмеженої функції

Якщо функція f(x) необмежена на відрізку [a;b], але інтегрована на кожному відрізку та існує ( ), то число І називають значенням невласного інтеграла і записують . Якщо при цьому І,то говорять також, що невласний інтеграл збіжний. Якщо І=, або зазначена границя не існує, то невласний інтеграл називають розбіжним.

Приклад 26. Дослідити на збіжність інтеграл .

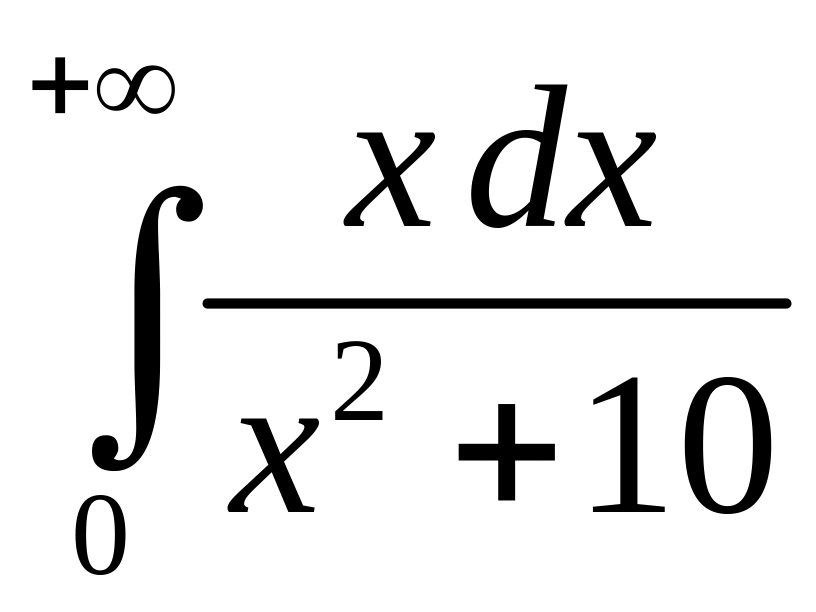Розв’язання.

Відповідь. Невласний інтеграл розбіжний.

Приклад 27. Дослідити на збіжність інтеграл .

Розв’язання. На проміжку інтегрування виберемо довільну точку. Наприклад, . Тоді будемо знаходити збіжність інтеграла на двох проміжках та . Одержимо

2.2.2. Застосування визначених інтегралів до задач геометрії

• Площу криволінійної трапеції для неперервної на сегменті [a;b] функції у=f(x)>0, згідно геометричного змісту інтеграла, обчислюють за формулою

• Площу криволінійного сектора в полярній системі координат обчислюють за формулою де 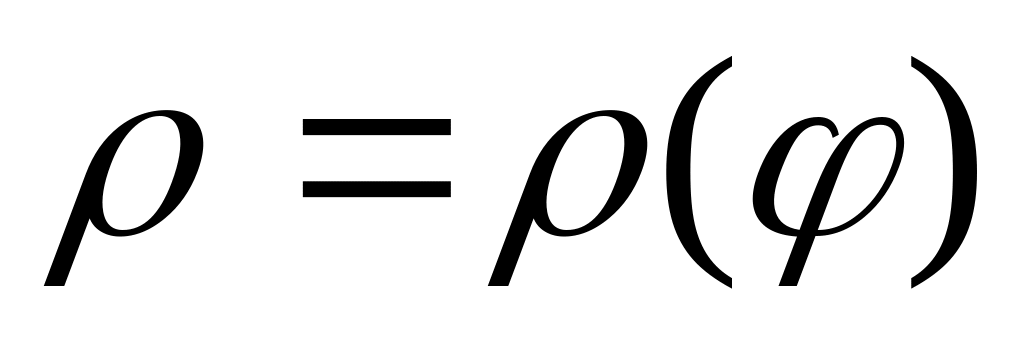неперервна функція.

• Довжину дуги лінії на сегменті [a;b] неперервної разом зі своєю похідною функції у=f(x) обчислюють за формулою

або за формулою , якщо функція задана параметрично x=x(t), y=y(t), t[t₁; t₂].

У випадку, коли крива задана полярним рівнянням , то

• Об’єм тіла обертання криволінійної трапеції з основою [a;b] навколо осі 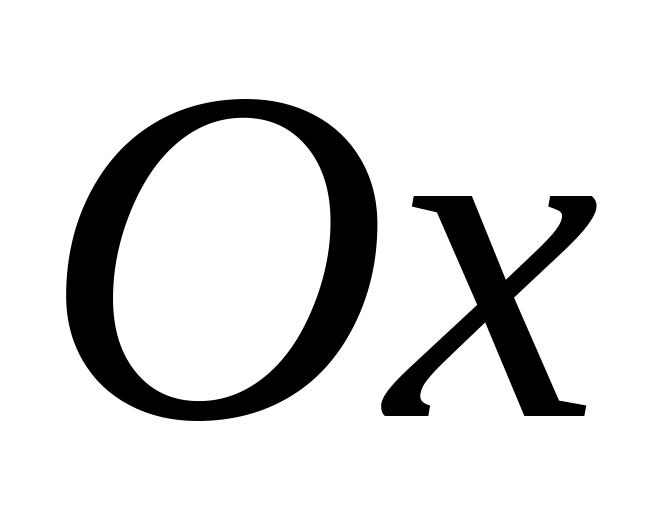, яка обмежена неперервною функцією у=f(x), обчислюється за формулою .

Якщо криволінійна трапеція з основою [c;d] обертається навколо осі , то об’єм тіла обертання обчислюють за формулою

, де неперервна для всіх y[c;d]

Приклад 28. Обчислити площу фігури, яка обмежена лініями та .

Розв’язання. Зобразимо фігуру.

Знайдемо точки перетину ліній. Для цього розв’яжемо систему:

.

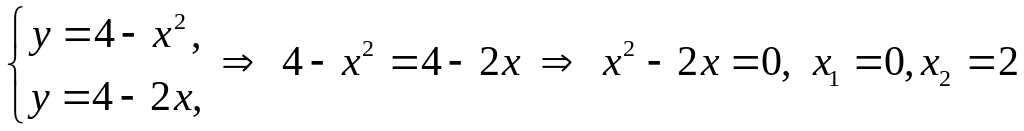Площа фігури дорівнює різниці площ двох криволінійних трапецій, площі яких обчислимо за формулою. Одержимо

Приклад 29. Обчислити площу фігури, яка обмежена лінією .

Р озв’язання. Побудуємо в полярних координатах лінію по точках Застосуємо формулу для обчислення площі криволінійного сектора в полярній системі координат. Одержимо

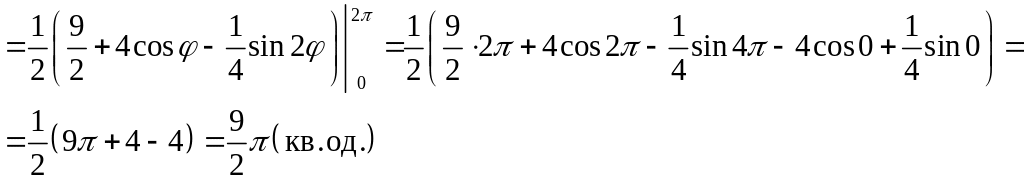
Приклад 30. Обчислити довжину дуги лінії , якщо .

Розв’язання. Згідно формули необхідно знати похідну функції. Знайдемо . Тоді

Приклад 31. Обчислити довжину однієї арки циклоїди

.

Розв’язання. Довжину дуги лінії обчислимо за формулою .Для цього знайдемо та , а також . Одержимо

Приклад 32.

Рис. 11

Обчислити об’єми тіл обертання навколо осей та фігури, яка обмежена лініями 4у=х² та у=х.

Розв’язання. Обчислимо об’єми тіл, які утворюються при обертанні фігури навколо осей. Знайдемо точки перетину ліній:

Одержали дві точки А(0;0) та В(4;4). Зобразимо ці тіла схематично

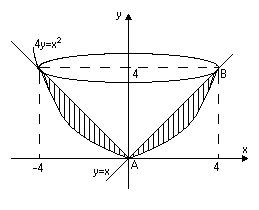
1) Об’єм тіла обертання навколо осі дорівнює різниці двох об’ємів тіл, які ми обчислимо за формулою .Одержимо

2) Аналогічно обчислюємо об’єм тіла обертання навколо осі .