28. Плотности распределения вероятностей.

1. Плотность распределения вероятностей – неотрицательная функция: . 2. Несобственный интеграл от плотности распределения вероятностей в пределах от   до   равен единице: .

Вероятностный смысл плотности распределения вероятности. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу  , приближенно равна (с точностью до бесконечно малых высшего порядка относительно  ) произведению плотности распределения вероятности в точке на длину интервала  : .

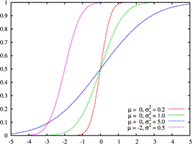
29. Непрерывная случайная величина, распределённая по нормальному закону. Правило трёх сигм.

Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами   и  (обозначают  ), если ее плотность вероятности имеет вид:

, где   ,   .
	Функция плотности  вероятности f(x)	Функция распределения F(x)
Рис.2. Нормальный закон распределения

Математическое ожидание характеризует центр рассеивания значений случайной величины и при изменении   кривая будет смещаться вдоль оси абсцисс (см. рис. 2 при   и при  ). Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, то кривая будет изменять свою форму, сжимаясь или растягиваясь (см. рис. 2 при  :  ;  ;  ). Таким образом, параметр   характеризует положение, а параметр  - форму кривой плотности вероятности.

Нормальный закон распределения случайной величины Х с параметрами   и   (обозначается N(0;1)) называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.

Правило трёх сигм ( ) — практически все значения нормально распределённой случайной величины лежат в интервале  . Более строго — не менее чем с 99,7 % достоверностью значениенормально распределенной случайной величины лежит в указанном интервале (при условии, что величина   истинная, а не полученная в результате обработки выборки).

Если же истинная величина   неизвестна, то следует пользоваться не  , а s. Таким образом, правило трёх сигм преобразуется в правило трёх s.

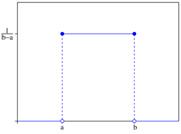
30. Непрерывная случайная величина, равномерно распределённая в интервале (a,b).

Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, т.е. f(x) имеет вид:

	Функция плотности  вероятности f(x)	Функция распределения F(x)
Рис.1. Равномерный закон распределения

Математическое ожидание  . Математическое ожидание случайной величины, равномерно распределенной на отрезке  (a, b), равняется середине этого отрезка.

         Дисперсия:

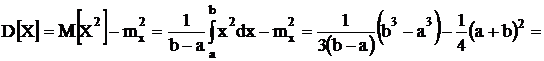
Величина     называется поправкой  Шеппарда.

 

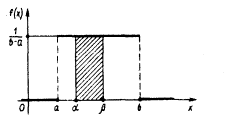
Вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (,), принадлежащий целиком отрезку [a, b]:

 

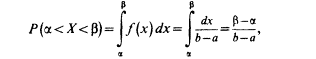
Геометрически эта вероятность представляет  собой  площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.