24. Основные свойства дисперсии.

 Основные   свойства   дисперсии :

•  дисперсия  любой случайной величины неотрицательна, D   0;

•  дисперсия  константы равна нулю, Dc=0;

• для произвольной константы D(c ) = c²D( );

•  дисперсия  суммы двух независимых случайных величин равна сумме их  дисперсий : D(  ) = D( ) + D (

25. Начальные и центральные моменты дискретной случайной величины.

 Начальным моментом k-го порядка α_k случайной величины Х называется математическое ожидание величиныХ^k, т.е. α_k = М(Х^k).      Начальный момент первого порядка – это математическое ожидание случайной величины.      Центральным моментом k-го порядка μ_k случайной величины Х называется математическое ожидание величины (Х–М(Х))^k, т.е. μ_k = М(Х–М(Х))^k.      Центральный момент второго порядка – это дисперсия случайной величины.      Для дискретной случайной величины начальный момент выражается суммой α_k =  , а центральный – суммой μ_k=   где р_i = p(X = x_i). Для начального и центрального моментов непрерывной случайной величины можно получить следующие равенства:      α_k =  μ ,_k =  ,      где φ(x) – плотность распределения случайной величины Х.

26. Непрерывные случайные величины. Функция распределения.

Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.

            Функцию распределения также называют интегральной функцией.

Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

27. Свойства функции распределения.

1. Значения функции распределения вероятностей принадлежат отрезку  : . 2. Функция распределения вероятностей – неубывающая функция, то есть: , если  . Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале  , равна приращению функции распределения вероятностей на этом интервале: . Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю. Используя последнее следствие, легко убедиться в справедливости следующих равенств: . 3. Если возможные значения непрерывной случайной величины принадлежат интервалу  , то: , если  ; , если  . Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения: ; . Плотностью распределения вероятностей непрерывной случайной величины   называют функцию   – первую производную от функции распределения вероятностей  : . Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей. Теорема. Вероятность того, что непрерывная случайная величина   примет значение, принадлежащее интервалу  , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах: . 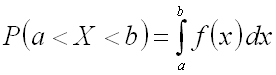Следовательно, зная плотность распределения вероятности  , можно найти функцию распределения   по формуле .