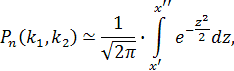Предмет теории вероятности. Испытание и событие. Классификация событий.
Предмет теории вероятностей
Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.
Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному. В природе нет ни одного физического явления, в котором не присутствовали бы в той или иной мере элементы случайности.
С чисто теоретической точки зрения те факторы, которые мы условно назвали «случайными», в принципе ничем не отличаются от других, которые мы выделили в качестве «основных». Теоретически можно неограниченно повышать точность решения каждой задачи, учитывая все новые и новые группы факторов: от самых существенных до самых ничтожных. Однако практически такая попытка одинаково подробно и тщательно проанализировать влияние решительно всех факторов, от которых зависит явление, привела бы только к тому, что решение задачи, в силу непомерной громоздкости и сложности, оказалось бы практически неосуществимым и к тому же не имело бы никакой познавательной ценности. Математические законы теории вероятностей – отражение реальных статистических законов, объективно существующих в массовых случайных явлениях природы. К изучению этих явлений теория вероятностей применяет математический метод и по своему методу является одним из разделов математики, столь же логически точным и строгим, как другие математические науки.
Испытание и событие.
Событие названо случайным, если при осуществлении определенной совокупности условий S оно может либо произойти, либо не произойти. В дальнейшем, вместо того чтобы говорить «совокупность условий S осуществлена», будем говорить кратко: «произведено испытание». Таким образом, событие будет рассматриваться как результат испытания.
Под испытанием понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат.
Пример 1. Стрелок стреляет по мишени, разделенной на четыре области. Выстрел — это испытание. Попадание в определенную область мишени — событие.
Классификация событий.
События можно подразделить на следующие три вида:
Достоверные
Невозможные
Случайные
Достоверным называется событие, которое обязательно произойдет, если будет осуществлен определенный комплекс условий
Например, закат солнца
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлен комплекс условий.
Например, свободный полет человека в условиях земли
Случайным называют событие, которое при осуществлении комплекса условий может либо произойти, либо не произойти.
Например, попадание молнии в дерево.
Классическое определение вероятности. Основные свойства.
Классическое определение вероятности
Вероятность – одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим.
ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Итак, вероятность события А определяется формулой:
где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.
Основные свойства.
Свойство 1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m=n, следовательно, P(A)=m/n=n/n=1
Свойство 2. Вероятность невозможного события равна нулю.
В этом случае m=0, следовательно, P(A)=m/n=0/n=0
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит 0<m/n<1, следовательно,
0<P(A)<1
Итак, вероятность любого события удовлетворяет двойному неравенству
0
P(A)
1
Относительная частота. Статистическое определение вероятности.
Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой
W (А) = m / n,
где m - число появлений события, n - общее число испытаний.
Сопоставляя определения вероятности и относительной частоты, заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта.
Статистическое определение вероятности. Вероятностью события А в данном испытании называется число Р(А), около которого группируются значения относительной частоты при больших n.
Так, в примере 2 вероятность в статистическом смысле равна 0,5. Таким образом, относительная частота события приближенно совпадает с его вероятностью в статистическом смысле, если число испытаний достаточно велико.
С этой точки зрения величина m = n Р(А) представляет собой среднее значение числа появления события А при n испытаниях.
Теорема сложения вероятностей несовместимых событию. Следствие.
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Доказательство. Докажем эту теорему для случая суммы двух несовместных событий А1и А2
Пусть событию А1 благоприятствуют m1 элементарных исходов, а событию А2-m2 исходов. Так как события А1и А2 по условию теоремы несовместны, то событию А1+ А2 благоприятствуют m1+m2
элементарных исходов из общего числа n исходов. Следовательно,
где
P(A1) вероятность события A? P(A2)- вероятность события A2
Следствие : Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
Определение. Противоположными называются два несовместных события, образующие полную группу.
Полная группа событий(определение), Теорема.
Полная группа событий - это несколько событий, из которых в результате опыта непременно должно появиться хотя бы одно из них, например, выпадение герба или цифры при бросании монеты.
Полная группа событий - такая группа событий, в которой хотя бы одно событие обязательно появится в результате эксперимента.
Теорема. Сумма вероятностей событий А1 , А2 , ..., Аn , образующих полную группу, равна единице:
Р (A1) + Р (А2) + ... + Р (Аn) = 1.
ДОКАЗАТЕЛЬСВО. Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то
Р (A1 + A2 + ... + An) = 1. (*)
Любые два события полной группы несовместны, поэтому можно применить теорему сложения:
Р (А1 + А2 + ... + Аn) = Р (A1) + Р (A2) + ... + Р (Аn). (**)
Сравнивая (*) и (**), получим
Р (А1) + Р (А2) + ... + Р (Аn) = 1.
Противоположные события(определение), Теорема.
Противоположными называют
два единственно возможных события,
образующих полную группу. Если одно из
двух противоположных событий обозначено
через A, то другое принято обозначать
Пример Из ящика наудачу взята деталь. События «появилась стандартная деталь» и «появилась нестандартная деталь» — противоположные.
Теорема. Сумма
вероятностей противоположных событий
равна единице:
Доказательство базируется на том, что противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице
З а м е ч а н и е 1. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают через q. Таким образом, в силу предыдущей теоремы
p + q = l
З
а м е ч а н и е 2. При решении задач на
отыскание вероятности события А часто
выгодно сначала вычислить вероятность
противоположного события, а затем найти
искомую вероятность по формуле
Произведение событий. События зависимые и независимые. Условная вероятность.
Произведение событий.
Определение: Произведением нескольких событий называется событие, состоящее в их совместном наступлении в результате испытания.
Произведение событий. Два события А и В называются независимыми, если вероятность одного из них не зависит от того, произошло или не произошло другое. Произведением независимых событий А и В называется событие С = А·В, заключающееся в том, что произошло и событие А, и событие В. Рассмотрим два независимых события А и В. Пусть событию А благоприятствуют m исходов из общего числа n исходов P(A)= m / n. Событию В - соответственно k и l исходов P(B)= k / l. Тогда для события С = А·В по правилу произведения благоприятных исходов будет m · k, а общее число - n · l. Вероятность произведения независимых событий равна произведению их вероятностей. P(AB)=P(A)·P(B) Например, вероятность выпадения двух гербов при бросании двух монет будет равна 0,5 · 0,5 = 0,25, а вероятность появления трех шестерок подряд при трех бросках игральной кости 1/6·1/6·1/6= 1/216.
Вероятность произведения зависимых событий. Пусть даны два зависимых события А и В. И из n равновозможных исходов событию А благоприятствуют m, событию В -k, событию АВ -r исходов (r m, r ). P(A)= m / n; P(B)= k / n; P(AB)= r / n. Если произошло событие А, то реализовался один из m исходов, благоприятствующих А. Вероятность того, что при этом условии произошло событие В найдется, как условная вероятность Отсюда P(AB)=P(A)·P(B/A). Это и есть правило умножения зависимых событий. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое произошло. P(AB)=P(A)·P(B/A).
Условная вероятность
Условной вероятностью Р(А/В) события А при условии, что событие В произошло (P(B)≠0) назовем отношение P(A*B)/P(B)
Теорема умножения вероятностей. Следствие1-4.
Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р (АВ) = Р (А) РA (В). (*)
Доказательство:
По определению условной вероятности,
РA (B) = Р (АВ) / Р (A).
Отсюда
Р (АВ) = Р (А) РA (В).
Следствие 1. Свойство независимости взаимно.
Следствие 2. Вероятность совместного появления нескольких событий, независмых в совокупности равна произведению вероятностей этих событий. p(A1,A2,...,Ak)=p(A1)p(A2)...p(Ak)
Если события A1,A2,...,Ak независмы в совокупности, то и противоположные им события также независимы.
Следствие 3. Вероятность появления хотя бы 1-го из событий A1,A2,...,Ak, независмых в совокупности равна разности между единицей и произведением вероятностей противоположных событий
p(A)=1−p(A1)p(A2)...p(Ak)
Формула полной вероятности.
Формула полной вероятности
Предположим,
что событие 
может
осуществляться только с одним из
несовместных событий 
.
Например, в магазин поступает одна и та
же продукция от трех предприятий в
разном количестве. Существует разная
вероятность выпуска некачественной
продукции на разных предприятиях.
Случайным образом отбирается одно из
изделий. Требуется определить вероятность
того, что это изделие некачественное
(событие
).
Здесь события
—
это выбор изделия из продукции
соответствующего предприятия.
В этом случае вероятность события можно рассматривать как сумму произведений событий
По теореме сложения вероятностей несовместных событий получаем
Используя теорему умножения вероятностей, находим
(3.1)
Формула (3.1) носит название формулы полной вероятности.
Формула Бейеса. Вероятность гипотез.
Формула Байеса
Пусть
событие
происходит
одновременно с одним из 
несовместных
событий
.
Требуется найти вероятность события 
,
если известно, что событие
произошло.
На основании теоремы о вероятности произведения двух событий можно написать
Откуда
или
(3.2)
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
Теорема сложения вероятностей совместных событий.
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р (А + В) = Р (А) + Р (В) - Р (АВ).
Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий Р(А + В+С) = Р(А) + Р(В) + + Р(С) - Р(АВ) - Р(АС) - Р(ВС) + Р(АВС).
Повторные независимые испытания. Схема Бернулли.
Схема Бернулли
Под
схемой Бернулли понимают конечную
серию 
повторных
независимых испытаний с двумя исходами.
Вероятность появления (удачи) одного
исхода при одном испытании обозначают 
,
а
непоявления (неудачи) его 
.
Я. Бернулли
установил, что вероятность ровно 
успехов
в серии из
повторных
независимых испытаний вычисляется по
следующей формуле:
То
значение 
,
при
котором число 
является
максимальным из множества {
},
называется наивероятнейшим,
и оно удовлетворяет условию
np
- q 
m
np+
p, 
Формулу
Бернулли можно обобщить на случай, когда
при каждом испытании происходит одно
и только одно из 
событий
с вероятностью 
( 
.
Вероятность
появления 
раз
первого события и 
-
второго
и 
-го
находится по формуле
При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:
Повторные независимые испытания.
повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два возможных исхода и вероятности исходов остаются неизменными для всех испытаний.
Рассмотрим случай многократного повторения одного и того же испытания или случайного эксперимента. Результат каждого испытания будем считать не зависящим от того, какой результат наступил в предыдущих испытаниях. В качестве результатов или элементарных исходов каждого отдельного испытания будем различать лишь две возможности:
Пусть вероятность P(A) появления события А постоянна и равна p (0 < .p < 1).
Пусть произведено n испытаний, которые мы будем рассматривать как один сложный случайный эксперимент.
Так как испытания независимы, то вероятность P каждого такого результата определяется путем перемножения вероятностей событий A и в соответствующих испытаниях.
Справедлива формула Бернулли:
По формуле Бернулли рассчитывается вероятность появления события A k раз в n повторных независимых испытаниях, где p - вероятность появления события A в одном испытании, q - вероятность появления события в одном испытании.
Сформулированные условия проведения испытаний иногда называются "схемой повторных независимых испытаний" или "схемой Бернулли"
Число k появления события A в n повторных независимых испытаниях называется частотой.
Локальная теорема Лапласа.
Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно m раз в n испытаниях, если число испытании достаточно велико.
Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Pn(m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n) значению функции
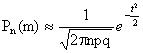
q=1-p, 
при m→∞ погрешность формулы →0.
Смысл пораметра t здесь среднее значение числа появления события А в m испытаниях.
Величина m-np есть отклонение числа появления события
-
некий
масштаб для отклонения при n испытаниях.
Величина t можно наглядно представить себе как отклонение числа появления событий А от среднего значения в масштабе σ.
Введём
функцию 
Тогда функция Лапласа запишется в виде:
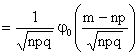
Интегральная теорема Лапласа.
Если
вероятность 
наступления
события 
в
каждом испытании постоянна и отлична
от нуля и единицы, то вероятность 
того,
что событие
появится
в 
испытаниях
от 
до 
раз,
приближенно равна определенному
интегралу
|
(4.1) |
где
и
Итак, вероятность того, что событие появится в независимых испытаниях от до раз,
где
и