Троичный сумматор
Так как возможно несколько видов физической реализации троичных систем: трёхуровневая однопроводная, двухуровневая двухразрядная двухпроводная, двухуровневая трёхразрядная одноединичная трёхпроводная, двухуровневая трёхразрядная однонулевая и др., то возможны и несколько видов троичных сумматоров.
Кроме этого, сумматоры в несимметричной троичной системе счисления отличаются логикой работы от сумматоров в симметричной троичной системе счисления.
Троичный одноразрядный полный сумматор в троичной несимметричной системе счисления является неполной тринарной (трёхоперандной) троичной логической функцией. Два операнда — два слагаемых — полные, третий операнд — троичный разряд переноса — неполный и имеет только два значения 0 и 1 из трёх.
В несимметричной троичной системе счисления
x0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
слагаемое |
x1 |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
слагаемое |
x2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Перенос из n-1 разряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
2 |
1 |
0 |
1 |
0 |
2 |
0 |
2 |
1 |
1 |
0 |
2 |
0 |
2 |
1 |
2 |
1 |
0 |
МЗР суммы, сумма по модулю 3 |
C |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
СЗР суммы, перенос в n+1 разряд |
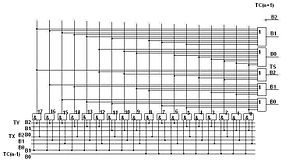
Троичный одноразрядный полный сумматор в трёхбитной одноединичной системе троичных логических элементов, работающий в троичной несимметричной системе счисления, приведённый на рисунке справа.
Троичный полный тринарный одноразрядный сумматор, работающий в троично симметричной системе счисления Фибоначчи, является полной тринарной троичной логической функцией с двухразрядным результатом.
В симметричной троичной системе счисления
x0 |
1 |
0 |
7 |
1 |
0 |
7 |
1 |
0 |
7 |
|
1 |
0 |
7 |
1 |
0 |
7 |
1 |
0 |
7 |
|
1 |
0 |
7 |
1 |
0 |
7 |
1 |
0 |
7 |
слагаемое |
|
x1 |
1 |
1 |
1 |
0 |
0 |
0 |
7 |
7 |
7 |
|
1 |
1 |
1 |
0 |
0 |
0 |
7 |
7 |
7 |
|
1 |
1 |
1 |
0 |
0 |
0 |
7 |
7 |
7 |
слагаемое |
|
x2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
Перенос из n-1 разряда |
Номер функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
0 |
7 |
1 |
7 |
1 |
0 |
1 |
0 |
7 |
|
7 |
1 |
0 |
1 |
0 |
7 |
0 |
7 |
1 |
|
1 |
0 |
7 |
0 |
7 |
1 |
7 |
1 |
0 |
МЗР суммы |
F3,-624603703776 |
C |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
|
0 |
0 |
0 |
0 |
0 |
7 |
0 |
7 |
7 |
СЗР суммы (трит переноса в n+1 разряд) |
F3,3483426737048 |
"7" обозначает "-1"
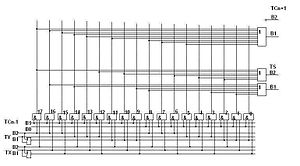
Троичный одноразрядный тринарный (трёхоперандный, полный) сумматор работающий в троичной симметричной системе счисления Фибоначчи в трёхбитной одноединичной системе троичных логических элементов с логическими элементами ИЛИ.
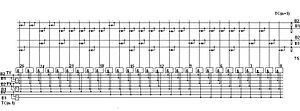
Троичный одноразрядный тринарный (трёхоперандный, полный) сумматор работающий в троичной симметричной системе счисления Фибоначчи в двухбитной системе троичных логических элементов с логическими элементами ИЛИ. Троичный зеркально-симметричный одноразрядный полный сумматор.
Принципиальная схема одноразрядного сумматора в несимметричной троичной системе счисления в трёхбитной одноединичной системе троичных логических элементов
Принципиальная схема троичного одноразрядного сумматора в двухбитной системе троичных логических элементов
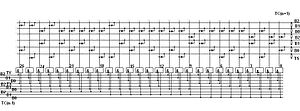
Принципиальная схема троичного полного одноразрядного сумматора, работающего в троичной симметричной системе счисления Фибоначчи в трёхбитной одноединичной системе троичных логических элементов
Принципиальная схема троичного полного сумматора в троичной симметричной системе счисления Фибоначчи в двухбитной системе троичных логических элементов