Полусумматор — логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S и C, где S — это бит суммы по модулю 2, а C — бит переноса. Однако, как можно заметить, для построения схемы двоичного сумматора (трёхразрядный сумматор, тринарный сумматор) необходимо иметь элемент, который суммирует три бита A, B и C, где C — бит переноса из предыдущего разряда, таким элементом является полный двоичный сумматор, трёхступенчатая разновидность которого состоит из двух полусумматоров и логического элемента 2ИЛИ.

История

• 1939 год — Джордж Штибиц (Georg Stibits) из компании Bell Laboratories создал первый двоичный полусумматор "Model K Аdder" на двух электромеханических реле

• 1958 год — в МГУ (мехмат) Н. П. Брусенцов построил первую электронную троичную ЭВМ «Сетунь» с первым электронным троичным полусумматором.

Двоичный полусумматор

Двоичный полусумматор может быть определён тремя способами: 1. табличным, в виде таблицы истинности, 2. аналитическим, в виде формулы (СДНФ), 3. графическим, в виде логической схемы. Так как формулы и схемы могут преобразовываться, то, одной таблице истинности двоичного полусумматора могут соответствовать множества различных формул и схем. Поэтому, табличный способ определения двоичного полусумматора является основным.

Двоичный полусумматор

Двоичный полусумматор представляет собой объединение двух бинарных (двухоперандных) двоичных логических функций: сумма по модулю два - S и разряд переноса при двоичном сложении - C.

x0=A	1	0	1	0
x1=B	1	1	0	0	Название действия (функции)	Номер функции
S	0	1	1	0	Бит суммы по модулю 2	F2,6
C	1	0	0	0	Бит переноса	F2,8

Ненулевой перенос образуется в 1-м случае из 4-х. СДНФ суммы по модулю 2: СДНФ бита переноса:

Полусумматор Штибица "Model k Аdder"

Полусумматор Штибица "Model K Аdder" состоит: из двух последовательно соединённых гальванических элементов, по 1,5 Вольта каждый, с суммарным напряжением 3 Вольта, двух кнопок для ввода двух битов аргументов A и B, двух электромагнитных реле, выполняющих бинарную двоичную логическую функцию сложения по модулю 2 и бинарную двоичную логическую функцию бита переноса при двоичном сложении, и двух лампочек накаливания с напряжением 3 Вольта для индикации бита суммы по модулю 2 (S) и бита переноса (C).

Троичный полусумматор

Так как существуют две троичных системы счисления - несимметричная, в которой в разряде переноса не бывает значения больше "1" и симметричная (Фибоначчи), в которой в разряде переноса возможны все три состояния трита, и, как минимум, три физических реализации троичных систем - трёхуровневая однопроводная, двухуровневая двухпроводная (BCT) и двухуровневая трёхбитная одноединичная, то и троичных полусумматоров может быть большое множество.

Троичный полусумматор в несимметричной троичной системе счисления представляет собой объединение двух бинарных троичных логических функций - «сложение по модулю 3» и «разряд переноса при троичном сложении».

x1=x	2	2	2	1	1	1	0	0	0
x0=y	2	1	0	2	1	0	2	1	0	Название действия (функции)	Номер функции
S	1	0	2	0	2	1	2	1	0	Трит суммы по модулю 3
C	1	1	0	1	0	0	0	0	0	Трит переноса

Троичный полусумматор в симметричной троичной системе счисления представляет собой объединение двух бинарных троичных логических функций - «младший разряд (трит) суммы (разности)» и «старший разряд (трит) суммы (разности) (разряд переноса при сложении в троичной симметричной системе счисления)».

x1=x	1	1	1	0	0	0	7	7	7
x0=y	1	0	7	1	0	7	1	0	7	Название действия (функции)	Номер функции
S	7	1	0	1	0	7	0	7	1	Младший трит суммы	F710107071=F-4160
C	1	0	0	0	0	0	0	0	7	Старший трит суммы (трит переноса)	F100000007=F6560

"7" обозначает "-1" Ненулевой перенос образуется в 2-х случаях из 9-ти. Троичный двухбитный двухпроводный бинарный (двухоперандный) одноразрядный

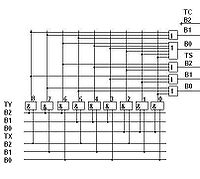
На рисунке справа приведена схема троичного несимметричного полусумматора в трёхбитной одноединичной системе троичных логических элементов.

Сумматор — устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов.