МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ СУМСЬКА ДЕРЖАВНИЙ УНІВЕРСИТЕТ КАФЕДРА ІНФОРМАТИКИ
Лабораторна робота №1 з дисципліни математична логіка та теорія алгоритмів
Виконав
Студент ПМ-11
Перевірив
Шаповалов С.П
Суми 2013
Зміст
Мета роботи 3
Хід виконання роботи 3
Опис алгоритму сортування злиттям 3
Реалізація зовнішньої процедури сортування злиттям на мові С++ 4
Швидкодія роботи сортування злиттям 5
Швидке сортування 6
6
Реалізація зовнішньої процедури сортування швидке на мові С++ 6
Результат роботи швидкого сортування 8
Приклад роботи програми 9
Сортування злиттям та швидке 10
Графічне представлення результатів 11
Висновок 12
Мета роботи
Ознайомитись з алгоритмами сортування злиттям та купою, навчитись їх програмувати. Засвоїти базовi прийоми тестування програм та вимiрювання їх ефективностi.
Хід виконання роботи
У даній роботі проводиться порівняльний аналіз двох видів сортування масивів натуральних чисел: сортування злиттям та сортування купою (пірамідальне сортування). На вхід надходять послідовності різних вхідних даних (послідовність з випадкових чисел, спадаюча послідовність, зростаюча послідовність). Для тестування подаються масиви різних розмірів (20, 50, 200, 1000, 2000, 5000, 7000). Числа взяті з проміжку[0,7000].
Опис алгоритму сортування злиттям
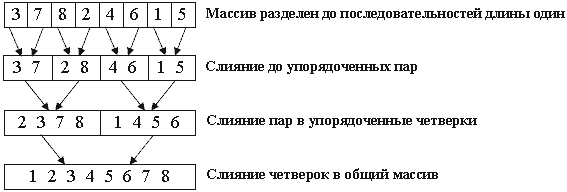
Роботу алгоритму можна розбити на два кроки:
Поділити масив на дві рівні частини і застосувати сортування злиттям до кожної з них.
Злити два відсортовані масиви з попереднього кроку у один таким чином, щоб він був відсортований.
Розглянемо кожний крок детальніше
Масив ділиться елементарним чином, а саме діленням націло пополам. Тобто якщо у нас парна кількість елементів (2n), то ми отримаємо два одинакові масиви (перший: 2n / 2 = n, а другий: 2n-n=n (загальна довжина мінус довжина першого)), якщо ж непарна (2n+1), то один з масивів буде на один елемент довший за інший (перший: (2n+1) / 2 = n, другий: (2n+1) - n = n+1). Потім застосовуємо функцію сортування на кожному з двох масивів.
У результаті попереднього кроку ми отримуємо два відсортовані масиви, які потрібно злити у один відсортований масив.
Реалізація зовнішньої процедури сортування злиттям на мові С++
void merge_sort(int low, int high, int *a){
int mid;
if(low < high){
por++;
mid = (low + high) / 2;
pr++;
merge_sort(low, mid, a);
merge_sort(mid + 1, high, a);
merge(low, mid, high, a);
}
}
Об'єднання двох відсортованих масивів у ході комбінування здійснюється за допомогою допоміжної процедури merge.
void merge(int low, int mid, int high, int *a){
int h, i, j, b[7000], k;
h = i = low;
j = mid + 1;
pr += 3;
while((h <= mid) && (j <= high)){
por+=2;
if(a[h] <=a [j]){
b[i] = a[h];
h++;
por++;
pr+=2;
} else {
b[i] = a[j];
j++;
pr+=2;
}
i++;
pr++;
}
if(h > mid){
por++;
pr++;
for(k = j; k <= high; k++){
por++;
pr++;
b[i] = a[k];
i++;
pr+=2;
}
} else {
pr++;
for(k = h; k <= mid; k++){
por++;
pr++;
b[i] = a[k];
i++;
pr+=2;
}
}
pr++;
for(k = low; k <= high; k++){
por++;
pr++;
a[k] = b[k];
pr++;
}
}