
- •Содержание
- •Введение
- •Выбор двигателя. Силовой и кинематический расчет привода.
- •Определение требуемой мощности электродвигателя.
- •Выбор электродвигателя
- •Определение общего передаточного числа привода и разбивка его по ступеням
- •Силовые и кинематические параметры привода
- •Межосевое расстояние передачи.
- •Модуль передачи, числа зубьев шестерни и колеса.
- •Основные размеры шестерни и колеса.
- •Выбор марки стали для изготовления зубчатых колес.
- •Степень точности передачи.
- •Определение сил, действующих в косозубом зацеплении цилиндрической передачи.
- •Проверочный расчет передачи на сопротивление контактной усталости активных поверхностей зубьев.
- •Допускаемые напряжения изгиба при расчете на сопротивлении усталости зубьев при изгибе.
- •Проверочный расчет передачи на сопротивление усталости при изгибе.
- •Проверочный расчет передачи на контактную прочность активных поверхностей в момент действия пиковой нагрузки (при кратковременной перегрузке).
- •Проверочный расчёт на изгибную прочность зубьев червячного колеса в момент действия пиковой нагрузки (при кратковременной перегрузке).
- •Расчет быстроходной ступени ступени редуктора
- •Выбор варианта термообработки зубчатых колес.
- •Допускаемые контактные напряжения при расчете зубчатой передачи на сопротивление контактной усталости активных поверхностей зубьев.
- •Основные параметры передачи.
- •Смещение в конической передачи.
- •Проверочный расчет передачи на сопротивление контактной усталости активных поверхностей зубьев.
- •2.2.6 Допускаемые напряжения изгиба при расчете на сопротивлении усталости зубьев при изгибе.
- •Проверочный расчет передачи на сопротивление усталости зубьев при изгибе.
- •Геометрический расчет конической передачи.
- •Выбор марки стали для изготовления зубчатых колес.
- •Проверочный расчет передачи на контактную прочность активных поверхностей в момент действия пиковой нагрузки (при кратковременной перегрузке).
- •Проверочный расчёт на изгибную прочность зубьев колеса в момент действия пиковой нагрузки (при кратковременной перегрузке).
- •Силы в зацеплении конической зубчатой передачи с прямыми зубьями.
- •Расчет открытой клиноременной передачи
- •Конструирование валов редуктора и предварительный выбор для них подшипников качения.
- •Выбор муфты
- •5. Конструирование колес редуктора и шкивов
- •5.1. Быстроходная ступень:
- •5.1.1. Конструктивные размеры колеса.
- •5.2. Тихоходная ступень:
- •5.2.1. Конструктивные размеры колеса.
- •5.3. Ременной передачи.
- •5.3.1. Ведущий шкив
- •5.3.2. Конструирование ведомого шкива.
- •Конструирование корпуса редуктора
- •Толщина стенок корпуса.
- •Конструктивное оформление фланцев корпуса .
- •Конструирование крышек подшипников.
- •Расчет соединений вал-ступица
- •Быстроходный вал.
- •Промежуточный вал.
- •Тихоходный вал.
- •Расчет тихоходного вала редуктора на сопротивление усталости
- •Расчет подшипников качения тихоходного вала на заданный ресурс.
- •Проектирование рамы привода
- •Использованные источники
Смещение в конической передачи.
В
связи с тем, что при разности твердости
активных поверхностей Н1-Н2>100НВ
принимаем
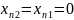 .
.
Коэффициенты тангенциального смещения:
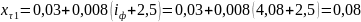 (111)
(111)
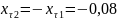 (112)
(112)
Проверочный расчет передачи на сопротивление контактной усталости активных поверхностей зубьев.
Уточним величину по формуле (94):
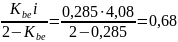
По табл. 2.14. [1] для .
Средняя окружная скорость зубчатых колес передачи:
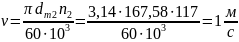 (113)
(113)
Тогда по табл. 2.11. [1] принимаем 9-ю степень точности передачи.
Коэффициент , учитывающий внутреннюю динамическую нагрузку при расчете по контактным напряжениям, принимаем по табл. 2.13. [1] равным .
Окружная сила в зацеплении при :
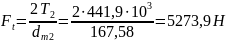 (114)
(114)
Тогда расчетные контактные напряжения:
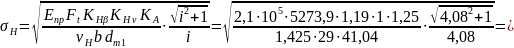
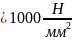 (115)
(115)
Сопротивление контактной усталости активных поверхностей зубьев обеспечивается, так как выполняется условие:
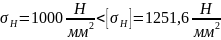 (116)
(116)
2.2.6 Допускаемые напряжения изгиба при расчете на сопротивлении усталости зубьев при изгибе.
Предел выносливости зубьев по напряжениям изгиба , соответствующей абсциссе точки перелома кривой усталости для напряжений изгиба, по табл. 2.4. [1] для варианта т.о. IV:
Для
шестерни (т.о. улучшение + цементация +
закалка)
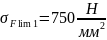 ;
;
Для
колеса (т.о. улучшение + закалка ТВЧ) при
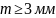
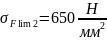
 Коэффициент
безопасности
по табл. 2.4. [1]: для шестерни
Коэффициент
безопасности
по табл. 2.4. [1]: для шестерни
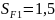 ;
для колеса
;
для колеса
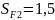 .
.
Коэффициент приведения по табл. 2.3. [1]:
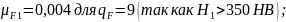
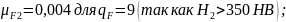
Эквивалентное число циклов нагружения при расчете по напряжениям изгиба для шестерни и колеса при числе зацеплений за один оборот зуба шестерни и зуба колеса :
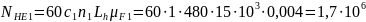 (117)
(117)
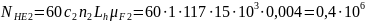 (118)
(118)
Базовое число циклов нагружения (абсцисса точки перелома кривой усталости для напряжения изгиба) для всех видов термообработки , тогда:
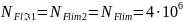 (119)
(119)
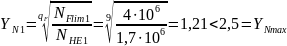 (120)
(120)
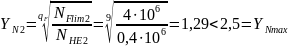 (121)
(121)
Коэффициент , учитывающий двухстороннее приложение нагрузки, принимаем равным , так как передача не реверсивная.
Тогда допустимые напряжения изгиба по формуле:
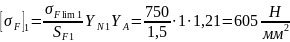 (122)
(122)
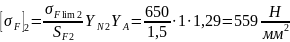 (123)
(123)
Проверочный расчет передачи на сопротивление усталости зубьев при изгибе.
По
табл. 2.14. [1] для
и роликовых опор при твердости активных
поверхностей зубьев (Н1>45HRCЭ
и Н2>45HRCЭ)
для передачи с прямыми зубьями коэффициент
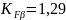 .
.
Коэффициент
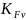 ,
учитывающий внутреннюю динамическую
нагрузку, принимаем по табл. 2.13. [1] равным
,
учитывающий внутреннюю динамическую
нагрузку, принимаем по табл. 2.13. [1] равным
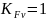 .
.
Коэффициент
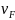 учитывающий влияние вида зубьев
конической передачи, для конической
передачи с круговыми зубьями определим
по формуле:
учитывающий влияние вида зубьев
конической передачи, для конической
передачи с круговыми зубьями определим
по формуле:
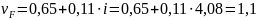 (124)
(124)
Числа
зубьев эквивалентных цилиндрических
прямозубых колес (эквивалентное число
зубьев)
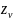 :
:
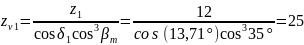 (125)
(125)
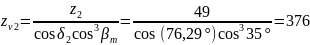 (126)
(126)
Коэффициент формы зуба и концентрации напряжений , согласно рис. 2.20. [1] в зависимости от числа зубьев z при коэффициенте смешения исходного контура х: для шестерни ; для колеса .
Тогда расчетные напряжения при изгибе в опасном сечении зуба шестерни и колеса конической передачи будут:
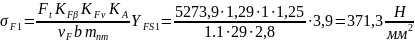 (127)
(127)
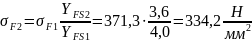 (128)
(128)
Сопротивление усталости зубьев при изгибе обеспечивается, так как выполняется допустимое условие:
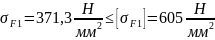 (129)
(129)
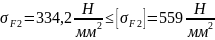 (130)
(130)
Геометрический расчет конической передачи.
Окружная толщина зуба в расчетном сечении
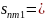
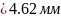 (131)
(131)
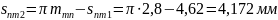 (132)
(132)
Внешняя высота головки зуба:
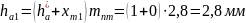 (133)
(133)
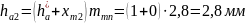 (134)
(134)
Внешняя высота ножки зуба:
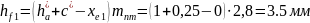 (135)
(135)
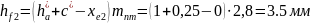 (136)
(136)
Угол ножки зуба:
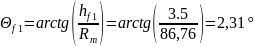 (137)
(137)
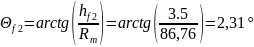 (138)
(138)
Угол головки зуба:
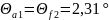 (139)
(139)
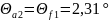 (140)
(140)
Угол конуса вершин:
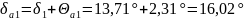 (141)
(141)
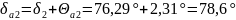 (142)
(142)
Угол конуса впадин:
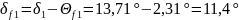 (143)
(143)
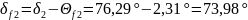 (144)
(144)
Увеличение высоты головки зуба при переходе от расчетного сечения на внешний торец:
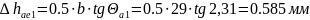 (145)
(145)
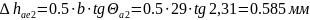 (146)
(146)
Внешняя высота головки зуба:
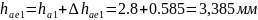 (147)
(147)
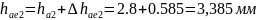 (148)
(148)
Увеличение высоты ножки зуба при переходе от расчетного сечения на внешний торец:
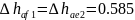 и
и
Внешняя высота головки зуба:
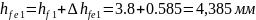 (149)
(149)
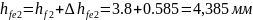 (150)
(150)
Внешняя высота зуба:
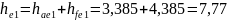 мм (151)
мм (151)
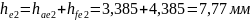 (152)
(152)
Расчет выполнен правильно, так как:
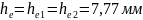 (153)
(153)
Внешний диаметр вершин зубьев:
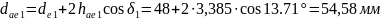 (154)
(154)
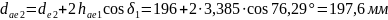 (155)
(155)
Внешний диаметр впадин зубьев:
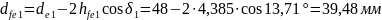 (156)
(156)
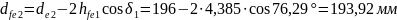 (157)
(157)
Расчетное базовая расстояние (от вершины делительного конуса по плоскости, в которой расположена внешняя окружность вершин зубьев):
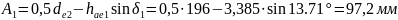 (158)
(158)
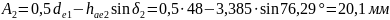 (159)
(159)
