13. Проверочный расчёт на изгибную прочность зубьев червячного колеса в момент действия пиковой нагрузки (при кратковременной перегрузке).

Предельные допускаемые напряжения изгиба при проверке на пиковую нагрузку по табл. 2.4. [1]:

Для шестерни (т.о. улучшение + цементация + закалка):

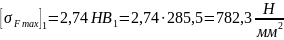
Для колеса (т.о. улучшение ):

Расчетные максимальные напряжения при изгибе 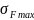в опасном сечении зуба шестерни и колеса при пиковой нагрузке:

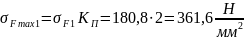(79)

(80)

Изгибная прочность зубьев шестерни и колеса в момент действия пиковой нагрузки при пиковой нагрузке обеспечивается, так как выполняется условия:

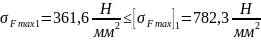(81)

(82)

2. Расчет быстроходной ступени ступени редуктора

   1. Выбор варианта термообработки зубчатых колес.

Для конической передачи с круговым зубом, с целью повышения нагрузочной способности передачи и обеспечения компактности привода по табл. 2.2. [1] принимаем вариант термообработки (т.о) IV: т.о. шестерни – улучшение + цементация + закалка, твердость активной поверхности зубьев 56…63 HRC_Э; т.о. колеса – улучшение + закалка ТВЧ, твердость активной поверхности зубьев 45…50 HRC_Э;

Средняя твердость активной поверхности зуба Н по формулам:

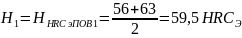(83)

(84)

2. Допускаемые контактные напряжения при расчете зубчатой передачи на сопротивление контактной усталости активных поверхностей зубьев.

Предел контактной выносливости активной поверхностей зубьев , соответствующей абсциссе точки предела перелома кривой усталости для контактных напряжений, по табл. 2.4. [1] для варианта т.о IV по формулам (15) и (16)

(85)

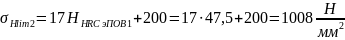(86)

Коэффициент безопасности по табл. 2.4. [1]:

;

Коэффициент приведения по табл. 2.3. [1]: для среднего нормального типового режима нагружения

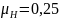
Эквивалентное число циклов нагружения для шестерни и колеса при числе зацеплений за один оборот зуба шестерни и зуба колеса :

(87)

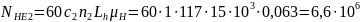(88)

Базовое число циклов нагружения (абсцисса точки перелома кривой усталости для контактных напряжений) по формуле для варианта т.о. IV по формулам:

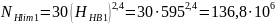(89)

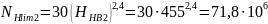(90)

Согласно полученных значения и не должны превышать . Это условие не выполняется для , тогда принимаем

Для определения долговечности воспользуемся формулой:

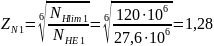(91)

(92)

В связи с тем, что и не превышают при , то принимаем 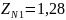и .

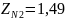Тогда допускаемые контактные напряжения согласно формуле для принятого варианта т.о. IV по формулам:

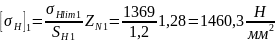(92)

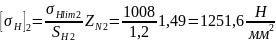(93)

Так как, меньше , то принимаем

3. Основные параметры передачи.

Принимаем коэффициент ширины 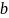зубчатого венца относительно внешнего конусного расстояния равным .

Определим величину:

(94)

По табл. 2.14. [1] для 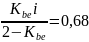и роликовых опор при твердости активных поверхностей зубьев (Н₁>45HRC_Э и Н₂>45HRC_Э) для передачи с круговыми зубьями коэффициент . Коэффициент внешней динамической нагрузки согласно п.2.2.3. принимаем . Коэффициент учитывающий влияние вида зубьев конической передачи, для конической передачи с круговыми зубьями определим по формуле:

(95)

При приведенном модуле упругости для стали и вращающем моменте на колесе ступени внешний делительный диаметр колеса прямозубой конической передачи (предварительно):

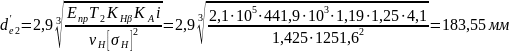(96)

Внешний делительный диаметр конической шестерни (предварительно):

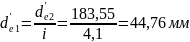(97)

По графику рис. 2.22.б [1] принимаем число зубьев для конической шестерни с круговым зубом 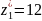. Окончательно принимаем в зависимости от активной поверхностей зубьев при Н₁>45HRC_Э и Н₂>45HRC_Э, согласно таблицы 2.16. [1] .

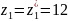При этом выполняется условие:

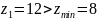
Где для круговых зубьев при 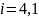, согласно таблицы 2.17. [1].

Число зубьев колеса:

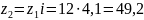(98)

Внешний окружной модуль:

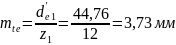(99)

По табл. 2.10. [1] принимаем стандартное значение 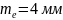(2-й ряд).

Уточняем внешние делительные диаметры колеса шестерни и колеса :

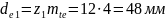(100)

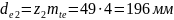(101)

Углы делительных конусов шестерни и колеса :

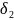(102)

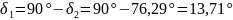(103)

Внешнее делительное конусное расстояние:

(104)

Ширина зубчатого венца шестерни и колеса:

(105)

При этом не должна превосходить значения 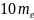, тогда:

(106)

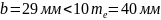
Принимаем .

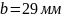Уточняем коэффициент :

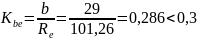(105)

Величина принята верно.

Среднее делительное конусное расстояние:

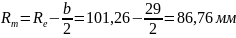(106)

Средний окружной модуль:

(107)

Средний нормальный модуль при

(108)

Средний делительный диаметры шестерни и колеса:

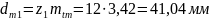(109)

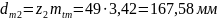(110)