3.2.2. Криптоалгоритм Рабина

Схема Рабина похожа на RSA, но возводит сообщение m не в высокую степень е, а в квадрат: c=m² mod n (число n так же как и в схеме RSA является произведением двух больших простых чисел p и q). На приемной стороне возможно декодирование сообщения и по схеме шифрования RSA, но чаще применяется несколько более быстрое извлечение квадратного корня по модулю n.

Процедура извлечения квадратного корня при известном разложении n на сомножители требует полиномиальное время, а при отсутствии подобной информации – гораздо более трудоемкая. Если p и q выбраны так, что отстаток от деления на 4 и у первого, и у второго числа равен трем, то вычисление квадратного корня производится по следующим формулам:

• алгоритм Евклида решается в целых числах уравнения a  p + b  q = 1;

• ;

• ;

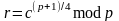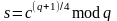• х=(а  p s + b  q  r) mod n;

• y=(а  p  s - b  q  r) mod n;

• корнями числа с являются 4 значения: (х mod n) и (у mod n).

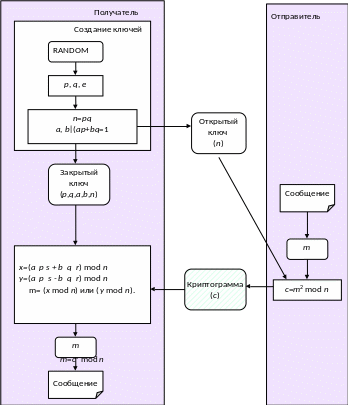
Преимущество схемы Рабина заключается в уменьшении открытого ключа: он состоит из одного числа n, что значительно ускоряет процесс шифрования. Недостатком является получение в результате извлечения квадратного корня на приемной строне четырех различных значений: m₁, m₂, m₃, m₄. Одно из этих значений действительно является зашифрованным текстом, три других – издержки модульной арифметики. Это свойство требует добавлять перед шифрованием в сообщение какие-либо метки, т.е. применять избыточное кодирование с тем чтобы алгоритм на приемной стороне с высокой вероятностью мог распознать среди четырех значений действительно верный вариант. Схема Рабина представлена на рис. 32.

Свободный досуп

Рис. 32. Криптосхема Рабина

3.2.3. Криптоалгоритм Эль Гамаль

Эль Гамаль: структура

Асимметричная схема предложена автором как логичное продолжение алгоритма обмена ключами Диффи-Хелмана. Она использует ту же операцию возведения в степень по модулю простого числа, но трудноразрешимой для злоумышленника задачей ставит отыскание не числа, которое возведено в степень, а то, в какую степень возведено известное число. Эта задача носит название проблемы дискретного логарифма.

Первый этап – создание пары ключей:

1. Выбирается произвольное, достаточно большое простое число p.

2. Для этого простого числа определяется любой образующий элемент, т.е. такое число а, при многократном возведении которого в степень по модулю р (a¹ mod p, a² mod p,…) будут перебираться все числа от 1 до (p-1) включительно в произвольном порядке, но обязательно только по одному разу.

3. Генерируется произвольное случайное число х (0<х<р) - это и есть закрытй ключ.

4. Вычисляется значение b=a^x mod p – комбинация (a,p,b) представляет собой открытый ключ получателя.

Ворой этап – шифрование с помощью окрытого ключа:

1. Отправитель генерирует произвольное случайное число у (0<у<р).

2. Помещает в начало шифрограммы число (a^y mod p).

3. Вычисляет величину k =(b^y mod p)=((a^x mod p)^y mod p).

4. Используя некоторую, заранее оговоренную в данной реализации, часть k в качестве симметричного ключа для любого блочного шифра шифрует отправляемое сообщение.

5. Забывает числа y и k - надежно стерев их из оперативной памяти и других мест, куда они могут случайно попасть.

Третий этап – дешифрование послания с помощью секретного ключа:

1. По приходу зашифрованного сообщения получатель отделяет от пакета величину (a^y mod p) и вычисляет на ее основе ((a^y mod p))^х mod p) – математика доказывает, что полученное число будет равно тому самому k, которое вычислил отправитель, так как в данной формуле операнды x и y можно менять местами.

2. Выделив из k ту же самую часть, что и отправитель, получатель дешифрует весь идущий далее пакет симметричным алгоритмом.

Общий вид системы приведен на рис. 33.

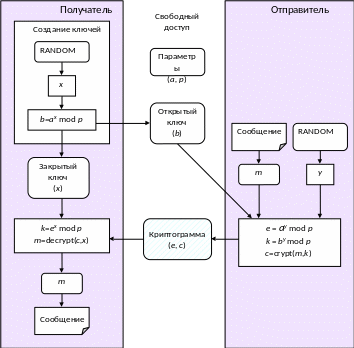
Рис. 33. Криптосистема Эль Гамаль

Схема Эль Гамаль: анализ

Проблема дискретного логарифмирования состоит в том, что, зная основание степени и получившейся после возведения результат по модулю простого числа, невозможно за полиномиальное время определить, в какую именно степень было возведено основание. В схеме Эль Гамаль потенциальный злоумышленник может получить значения a,p, (a^x mod p) и (a^у mod p). Однако из-за сложности определения чисел x и y «в чистом виде» у него не оказывается возможности вычислить значение k=(a^xy mod p), которое ему необходимо для прочения шифровки.

Относительно числа p криптоанализ выдвигает следующие требование. Число (p-1) должно содержать в разложении на множители большой простой делитель. В некоторых протоколах с участием схемы Эль Гамаль p выбирается как (q2+1), где q – простое число. При выборе x и y получателем и отправителем соответственно, естественно, должно выполняться требование к их информационной емкости. Для генерации этих чисел должен использоваться криптостойкий генератор случайных чисел. В противном случае злоумышленник может определить x или y полным перебором.

По криптостойкости в схеме Эль Гамаль 512-битное число p приравнивается к 56-битному симметричному ключу. Поэтому на практике применяются p длиной в 768, 1024 и 1536 бит.

Схема Эль Гамаль: пример

В качестве простого числа, порождающего циклическую группу, выберем p=11, за образующий элемент примем число а=7 (при возведении 7 в степень 1,2,3 и т.д. по модулю 11 последовательно проходят все 10 значений [7,5,2,3,10,4,6,9,8,1]). Секретным ключом х выберем 6, параметр b принимает значение b=(a^x mod p)=7⁶ mod 11)=4. В целом открытый ключ принимает вид (а=7, p=11, b=4).

Предположим, что некий абонент хочет передать сообщение. Он выбрал случайное число, не превосходящее p, например, y=9. В начало шифрограммы помещается число (a^у mod p)=7⁹ mod 11)=8. Кроме того, на основании у и открытого ключа отправитель вычисляет k=b^y mod p=4⁹ mod 11=3. Выбрав значение 3 или какие-либо его биты в качестве симметричного ключа, отправитель шифрует передаваемые данные и стирает величины 9 и 3 со своих накопителей.

Получатель по приходу пакета для вычисления k=(a^y mod p)^х, mod p возводит число 8 из заголовка шифрограммы в степень секретного ключа и получает k=8⁶ mod 11=3 – то же самое значение, которое использовал отправитель, шифруя собственно данные.