12.Непрерывно-стохастические модели. Q - схемы. Основные понятия обслуживания. Понятие прибора обслуживания.

Непрерывно-стохастический подход рассмотрим на основе систем массового обслуживания, которые будем называть Q – схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

В качестве процесса обслуживания могут быть представлены процессы функционирования экономических, технических, производственных и других систем.

Характерным для работы таких объектов является стохастический характер процесса их функционирования, т.е. случайное появление заявок на обслуживание и завершение обслуживания в случайные моменты времени.

В любом элементарном акте обслуживания можно выделить две основные составляющие:

1.Ожидание обслуживания заявкой;

2.Собственно обслуживания заявки.

Э то можно изобразить в виде некоторого i-го прибора обслуживания П_i, состоящего из накопителя заявок Н_i, канала обслуживания К_i.

В накопителе заявок может одновременно находится 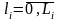заявок, где L_i – емкость i-го накопителя.

На каждый прибор обслуживания П_i поступают потоки событий:

- в накопитель Н_i потоки заявок ω_i ;

- в канал К_i – поток обслуживаний U_i .

Потоком событий называется последовательность событий, происходящих одно за другим в случайные моменты времени.

Различают потоки однородных и неоднородных событий.

Поток событий называется однородным, если он характеризуется только моментами наступления этих событий (вызывающими моментами) и задаются последовательностью {t_n} = {0 ≤ t₁ ≤ t₂ … ≤ t_n ≤ …},

где t_n – момент наступления n-го события.

Однородный поток событий может быть задан также в виде последовательности промежутков времени между n-м и (n-1)-м событиями {τ_n}, которая однозначно связана с последовательностью вызывающих моментов {t_n} следующим образом: τ_n = t_n – t_n-1, Например, при n = 1 и t_o = 0, τ₁ = t₁;

при n = 2 τ₂ = t₂ - t₁. и т.д.

Потоком неоднородных событий называется последовательность {t_n, f_n}, где t_n – вызывающие моменты; f_n – набор признаков события (наличие приоритета; возможность обслуживания тем или иным типом канала и т.д.).

Заявки, обслуженные каналом К_i, и заявки, покинувшие прибор П_i по различным причинам необслуженными (например, из-за переполнения накопителя), образуют выходной поток y_i  Y.

П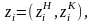 роцесс функционирования прибора обслуживания П_i можно представить как процесс изменения состояний его элементов во времени z_i(t). Переход в новое состояние для прибора П_i означает изменение количества заявок, которые в нем находятся (в канале К_j и накопителе Н_i).

Вектор состояний для прибора П_i имеет вид

где 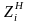- состояние накопителя (0 – накопитель пустой, n – в накопителе n заявка, L^н – накопитель заполнен);

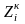- состояние канала (0 – канал свободен, 1 – канал занят, 2 – канал заблокирован).

13.Многоканальные и многофазные, разомкнутые и замкнутые q - схемы.

П ри моделировании систем, имеющих более сложные структурные связи и алгоритмы поведения, для формализации используются не отдельные приборы обслуживания, а Q-схемы, образуемые композицией многих элементарных приборов обслуживания П_i или их элементов.

Если k различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема).

Е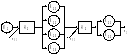 сли приборы П_i и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема).

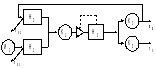С вязи между элементами Q-схемы изображают в виде стрелок (линий потока, отражающих направление движения заявок). Различают разомкнутые и замкнутые Q-схемы.

В замкнутых Q-схемах имеются обратные связи, по которым заявки перемещаются в направлении, обратном движению вход-выход.

В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент, т.е. обратная связь отсутствует.