10.Проверка качества псевдослучайных последовательностей чисел. Проверка стохастичности и независимости.
Проверка стохастичности последовательностей псевдослучайных чисел наиболее часто проводится методами комбинаций и серий.
Сущность метода комбинаций сводится к определению закона распределения длин участков между единицами (нулями) или закона распределения (появления) числа единиц (нулей) в п-
разрядном
двоичном числе
.
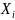На
практике длину последовательности
берут
достаточно большой и проверяют все и
разрядов или только
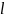старших
разрядов числа
.
Теоретически
закон появления у единиц в
разрядах двоичного числа
описывается
исходя из независимости отдельных
разрядов биномиальным законом
распределения:
где
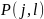— вероятность появления
единиц в
разрядах числа
;
— вероятность появления единицы (нуля)
в любом разряде числа
;
.
Тогда
при фиксированной длине выборки
теоретически
ожидаемое число появления случайных
чисел
с
единицами
в проверяемых
разрядах
будет равно
.
После
нахождения теоретических и экспериментальных
вероятностей
или чисел
при
различных значениях
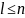гипотеза о стохастичности проверяется
с использованием критериев согласия.
При
анализе стохастичности последовательности
чисел
методом
серий последовательность разбивается
на элементы первого и второго рода (а и
b),
т.
е.
.
Серией называется любой отрезок последовательности, состоящий из идущих друг за другом элементов одного и того же рода, причем число элементов в отрезке (а или b) называется длиной серии.
После разбиения последовательности на серии первого и второго рода будем иметь, например, последовательность вида ...aabbbbaaabaaaabbbab... .
Так
как случайные числа а
и
b
в
данной последовательности независимы
и принадлежат последовательности
,
равномерно распределенной на интервале
(0, 1), то теоретическая вероятность
появления серии длиной
в
последовательности длиной
в
опытах
(под опытом здесь понимается генерация
числа
,
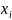и
проверка условия
)
определится
формулой Бернулли:
В
случае экспериментальной проверки
оцениваются частоты появления серий
длиной
.
В результате получаются теоретическая
и экспериментальная зависимости
,
сходимость
которых проверяется по известным
критериям согласия, причем проверку
целесообразно проводить при различных
значениях
,
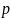и
.
Проверка независимости элементов последовательности псевдослучайных квазиравномерно распределенных чисел проводится на основе вычисления корреляционного момента.
Случайные
величины
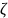и
называются
независимыми, если закон распределения
каждой из них не зависит от того, какое
значение приняла другая. Таким образом,
независимость элементов последовательности
может
быть проверена путем введения в
рассмотрение последовательности
,
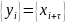где
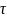— величина сдвига последовательностей.
В
общем случае корреляционный момент
дискретных случайных величин
и
с возможными значениями
,
и
определяется по формуле
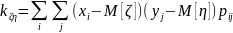
где
—
вероятность того, что
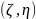примет значение
.
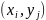Корреляционный
момент характеризует рассеивание
случайных величин
и
и их зависимость. Если случайные числа
независимы, то
.
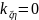Коэффициент
корреляции
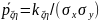
где
—
средние квадратические отклонения
величин
и
.
При
проведении оценок коэффициента корреляции
на ЭВМ удобно для вычисления использовать
следующее выражение:
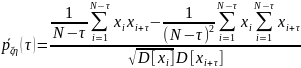
где
При
вычислениях сначала рационально
определить суммы:
При
любом
для достаточно больших
с
доверительной вероятностью
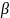справедливо соотношение
Если
найденное эмпирическое значение
находится в указанных пределах, то с
вероятностью
можно утверждать, что полученная
последовательность чисел
удовлетворяет
гипотезе корреляционной независимости.
11.Моделирование случайных процессов с заданной корреляционной функцией.