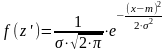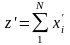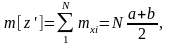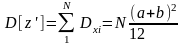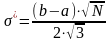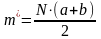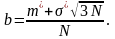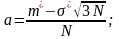- •2. Классификация методов и видов моделирования.
- •3. Математическое моделирование. Аналитические и имитационные модели.
- •4. Общая характеристика метода статистического моделирования. Области применения метода статистического моделирования
- •5.Методика оценки площади фигуры методом статистического моделирования.
- •6.Генерация и преобразование псевдослучайных последовательностей чисел. Аппаратный и табличный способы.
- •7.Получение псевдослучайных последовательностей чисел с равномерным в интервале [a,b] и показательным законами распределения.
- •8.Получение последовательностей псевдослучайных чисел, распределенных по нормальному закону с параметрами m и sg.
- •9.Проверка качества псевдослучайных последовательностей чисел. Проверка равномерности.
- •10.Проверка качества псевдослучайных последовательностей чисел. Проверка стохастичности и независимости.
- •12.Непрерывно-стохастические модели. Q - схемы. Основные понятия обслуживания. Понятие прибора обслуживания.
- •13.Многоканальные и многофазные, разомкнутые и замкнутые q - схемы.
- •14.Приоритеты в q - схемах. Статические и динамические, относительные и абсолютные приоритеты.
- •15.Принципы реализации моделирующих алгоритмов q - схем. Укрупненная схема детерминированного моделирующего алгоритма q – схемы
- •16.Реализация моделирующего алгоритма q - схемы. Алгоритм блока имитации обслуживания каналами фазы 3
- •17.Реализация моделирующего алгоритма q - схемы. Алгоритм блока имитации обслуживания каналами фазы 2
- •18.Реализация моделирующего алгоритма q - схемы. Алгоритм взаимодействия накопителя и каналов 2-ой фазы.
- •19.Реализация моделирующего алгоритма q - схемы. Алгоритм взаимодействия каналов 1-ой фазы и накопителя 2-ой фазы.
- •20.Реализация моделирующего алгоритма q - схемы. Алгоритм взаимодействия заявок в накопителе первой фазы и каналов 1-ой фазы.
- •21.Реализация моделирующего алгоритма q - схемы. Алгоритм взаимодействия источника заявок и накопителя первой фазы.
- •22.Особенности построения моделирующего алгоритма q - схемы по принципу dz.
- •23.Особенности построения асинхронного моделирующего алгоритма q - схемы.
- •24.Агрегативный подход к описанию процессов функционирования систем.
- •25.Понятие агрегата. Основные параметры (множества), характеризующие агрегаты. Описание процесса функционирования агрегата.
- •26.Структура агрегатной системы. Внутренняя и внешняя информация, циркулирующая в а - схемах.
- •27.Формирование процессов функционирования систем с использованием а - схем. Схема общего вида. Основные понятия.
- •28.Схемы и алгоритмы функционирования агрегатов "внешняя среда, "канал" и "накопитель" а - схем.
- •29.Схемы и алгоритмы функционирования агрегатов "распределитель" и "сумматор" а - схем.
- •29.2.Укрупненная схема моделирующего алгоритма а - схемы.
- •30.Общие вопросы планирования эксперимента. Полный факторный эксперимент. Формирование матрицы планирования эксперимента.
- •31.Планирование эксперимента. Проведение опытов и проверка воспроизводимости параллельных опытов.
- •32.Планирование эксперимента. Расчет коэффициентов регрессии и проверка их значимости.
- •33.Планирование эксперимента. Проверка адекватности математической модели.
- •34.Планирование эксперимента. Построение математической модели в натуральных единицах.
- •35.Планирование эксперимента. Понятие дробного факторного эксперимента. Построение матрицы планирования дробного факторного эксперимента.
- •37.Построение математических моделей по заданным экспериментальным данным. Анализ экспериментальных данных и выбор вида уравнения регрессии.
- •38.Построение математических моделей по заданным экспериментальным данным. Построение системы нормальных уравнений и математической модели.
- •39.Языки имитационного моделирования систем: simula, simscript, gpss и др. Имитационное моделирование систем на gpss/pc.
- •40.Функциональная структура gpss. Типы объектов: транзакты, блоки, списки, устройства, памяти, логические ключи, очереди, таблицы, ячейки, функции, переменные.
- •41.Понятие транзакта. Списки событий (текущих и будущих). Блоки gpss/pc, связанные с транзактами.
- •42.Блок generate создания транзакта. Его параметры и стандартные числовые атрибуты(сча). Пример использования блока generate.
8.Получение последовательностей псевдослучайных чисел, распределенных по нормальному закону с параметрами m и sg.
Функция плотности распределения последовательности случайных чисел, распределенных по нормальному закону имеет вид
|
(1) |
В силу центральной предельной теоремы случайная величина
|
(2) |
при достаточно большом будет иметь распределение, близкое к нормальному.
Если xi некоррелированные величины, то
|
(3) |
Используя
последние выражения для заданного
можно определить границы [a, b] такие,
чтобы
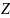 имела заданные значения параметров
имела заданные значения параметров
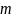 и
и
 ,
решив систему уравнений:
,
решив систему уравнений:
|
(4) |
откуда:
|
(4) |
Для получения псевдослучайных чисел xi, равномерно распределенной на интервале [a, b] следует использовать преобразование:
|
(5) |
Используя аппарат функциональных преобразований, а также размножение функции в ряды специального вида, можно получить уточненную формулу для формирования последовательностей случайных чисел, распределенных по нормальному закону:
|
(6) |
9.Проверка качества псевдослучайных последовательностей чисел. Проверка равномерности.
П роверка
равномерности последовательностей
псевдослучайных квазиравномерно
распределенных чисел
роверка
равномерности последовательностей
псевдослучайных квазиравномерно
распределенных чисел
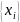 может быть выполнена по гистограмме с
использованием косвенных признаков.
Суть проверки по гистограмме сводится
к следующему. Выдвигается гипотеза о
равномерности распределения чисел в
интервале (0,1). Затем интервал (0,1)
разбивается на
равных
частей, тогда при генерации последовательности
каждое из чисел х
с
вероятностью
может быть выполнена по гистограмме с
использованием косвенных признаков.
Суть проверки по гистограмме сводится
к следующему. Выдвигается гипотеза о
равномерности распределения чисел в
интервале (0,1). Затем интервал (0,1)
разбивается на
равных
частей, тогда при генерации последовательности
каждое из чисел х
с
вероятностью
 попадает в один из подынтервалов. Всего
в каждый
попадает в один из подынтервалов. Всего
в каждый
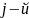 подынтервал
попадает
подынтервал
попадает
 чисел
последовательности
чисел
последовательности
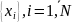 ,
причем
,
причем
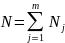 .
Относительная
частота попадания случайных чисел
последовательности
в каждый из подынтервалов будет равна
.
Относительная
частота попадания случайных чисел
последовательности
в каждый из подынтервалов будет равна
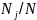 .
.
В
виде
соответствующей гистограммы пунктирная
линия соответствует теоретическому
значению
 ,
а
сплошная — экспериментальному
.
Очевидно,
что если числа х, принадлежат псевдослучайной
квазиравномерно распределенной
последовательности, то при достаточно
больших
экспериментальная
гистограмма приблизится к теоретической
прямой
,
а
сплошная — экспериментальному
.
Очевидно,
что если числа х, принадлежат псевдослучайной
квазиравномерно распределенной
последовательности, то при достаточно
больших
экспериментальная
гистограмма приблизится к теоретической
прямой
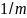 .
.
Оценка степени приближения, т. е. равномерности последовательности ,
может быть проведена с использованием критериев согласия. На практике обычно
принимается
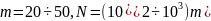 .
.
Суть проверки равномерности по косвенным признакам сводится к следующему. Генерируемая последовательность чисел разбивается на две последовательности:
|
|
З атем
проводится следующий эксперимент. Если
выполняется условие
атем
проводится следующий эксперимент. Если
выполняется условие
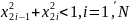 ,
то
фиксируется наступление некоторого
события и в счетчик событий добавляется
единица. После
,
то
фиксируется наступление некоторого
события и в счетчик событий добавляется
единица. После
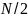 опытов, когда генерировано
число,
в счетчике будет некоторое число
опытов, когда генерировано
число,
в счетчике будет некоторое число
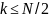 .
.
Геометрически
условие это означает, что точка
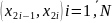 находится
находится
внутри
четверти круга радиусом
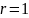 .
В
общем случае точка
.
В
общем случае точка
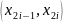 всегда попадает внутрь единичного
квадрата. Тогда теоретически вероятность
попадания этой точки в четверть круга
всегда попадает внутрь единичного
квадрата. Тогда теоретически вероятность
попадания этой точки в четверть круга
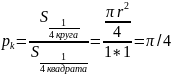 .
Если числа последовательности
равномерны, то в силу закона больших
чисел теории вероятностей при больших
относительная
частота
.
Если числа последовательности
равномерны, то в силу закона больших
чисел теории вероятностей при больших
относительная
частота
 .
.