
- •2. Классификация методов и видов моделирования.
- •3. Математическое моделирование. Аналитические и имитационные модели.
- •4. Общая характеристика метода статистического моделирования. Области применения метода статистического моделирования
- •5.Методика оценки площади фигуры методом статистического моделирования.
- •6.Генерация и преобразование псевдослучайных последовательностей чисел. Аппаратный и табличный способы.
- •7.Получение псевдослучайных последовательностей чисел с равномерным в интервале [a,b] и показательным законами распределения.
- •8.Получение последовательностей псевдослучайных чисел, распределенных по нормальному закону с параметрами m и sg.
- •9.Проверка качества псевдослучайных последовательностей чисел. Проверка равномерности.
- •10.Проверка качества псевдослучайных последовательностей чисел. Проверка стохастичности и независимости.
- •12.Непрерывно-стохастические модели. Q - схемы. Основные понятия обслуживания. Понятие прибора обслуживания.
- •13.Многоканальные и многофазные, разомкнутые и замкнутые q - схемы.
- •14.Приоритеты в q - схемах. Статические и динамические, относительные и абсолютные приоритеты.
- •15.Принципы реализации моделирующих алгоритмов q - схем. Укрупненная схема детерминированного моделирующего алгоритма q – схемы
- •16.Реализация моделирующего алгоритма q - схемы. Алгоритм блока имитации обслуживания каналами фазы 3
- •17.Реализация моделирующего алгоритма q - схемы. Алгоритм блока имитации обслуживания каналами фазы 2
- •18.Реализация моделирующего алгоритма q - схемы. Алгоритм взаимодействия накопителя и каналов 2-ой фазы.
- •19.Реализация моделирующего алгоритма q - схемы. Алгоритм взаимодействия каналов 1-ой фазы и накопителя 2-ой фазы.
- •20.Реализация моделирующего алгоритма q - схемы. Алгоритм взаимодействия заявок в накопителе первой фазы и каналов 1-ой фазы.
- •21.Реализация моделирующего алгоритма q - схемы. Алгоритм взаимодействия источника заявок и накопителя первой фазы.
- •22.Особенности построения моделирующего алгоритма q - схемы по принципу dz.
- •23.Особенности построения асинхронного моделирующего алгоритма q - схемы.
- •24.Агрегативный подход к описанию процессов функционирования систем.
- •25.Понятие агрегата. Основные параметры (множества), характеризующие агрегаты. Описание процесса функционирования агрегата.
- •26.Структура агрегатной системы. Внутренняя и внешняя информация, циркулирующая в а - схемах.
- •27.Формирование процессов функционирования систем с использованием а - схем. Схема общего вида. Основные понятия.
- •28.Схемы и алгоритмы функционирования агрегатов "внешняя среда, "канал" и "накопитель" а - схем.
- •29.Схемы и алгоритмы функционирования агрегатов "распределитель" и "сумматор" а - схем.
- •29.2.Укрупненная схема моделирующего алгоритма а - схемы.
- •30.Общие вопросы планирования эксперимента. Полный факторный эксперимент. Формирование матрицы планирования эксперимента.
- •31.Планирование эксперимента. Проведение опытов и проверка воспроизводимости параллельных опытов.
- •32.Планирование эксперимента. Расчет коэффициентов регрессии и проверка их значимости.
- •33.Планирование эксперимента. Проверка адекватности математической модели.
- •34.Планирование эксперимента. Построение математической модели в натуральных единицах.
- •35.Планирование эксперимента. Понятие дробного факторного эксперимента. Построение матрицы планирования дробного факторного эксперимента.
- •37.Построение математических моделей по заданным экспериментальным данным. Анализ экспериментальных данных и выбор вида уравнения регрессии.
- •38.Построение математических моделей по заданным экспериментальным данным. Построение системы нормальных уравнений и математической модели.
- •39.Языки имитационного моделирования систем: simula, simscript, gpss и др. Имитационное моделирование систем на gpss/pc.
- •40.Функциональная структура gpss. Типы объектов: транзакты, блоки, списки, устройства, памяти, логические ключи, очереди, таблицы, ячейки, функции, переменные.
- •41.Понятие транзакта. Списки событий (текущих и будущих). Блоки gpss/pc, связанные с транзактами.
- •42.Блок generate создания транзакта. Его параметры и стандартные числовые атрибуты(сча). Пример использования блока generate.
31.Планирование эксперимента. Проведение опытов и проверка воспроизводимости параллельных опытов.
Проверка воспроизводимости параллельных опытов при одинаковом их числе на каждом сочетании уровней факторов осуществляется по критерию Кохрена
 (1)
(1)
где
 - дисперсия, характеризующая рассеивание
результатов опытов на u–
м сочетании уровней факторов.
- дисперсия, характеризующая рассеивание
результатов опытов на u–
м сочетании уровней факторов.
Процесс считается воспроизводимым, если выполняется неравенство (1). Если же неравенство (1) не выполняется, то необходимо уточнить измерения в опытах с максимальными дисперсиями .
32.Планирование эксперимента. Расчет коэффициентов регрессии и проверка их значимости.
В случае воспроизводимости процесса переходят к расчету коэффициентов регрессии
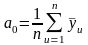
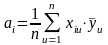
 .
.
Затем строят линейную модель эксперимента:
 .
.
Далее необходимо выполнить оценку значимости коэффициентов регрессии с помощью критерия Стьюдента. Коэффициент считается значимым, если выполняется неравенство
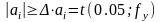
где
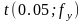 – табличное значение критерия Стьюдента.
– табличное значение критерия Стьюдента.
33.Планирование эксперимента. Проверка адекватности математической модели.
После расчета коэффициентов регрессии необходимо проверить адекватность модели с помощью критерия Фишера. Модель считается адекватной, если имеет место неравенство
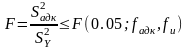
где

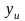 -
расчетное значение отклика в u -м опыте;
-
расчетное значение отклика в u -м опыте;
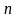 -
количество опытов;
-
количество опытов;
F(0,05, fадк fт) - критерий Фишера при 5% -м уровне зависимости;
fадк = n-k-1 - число степеней свободы дисперсии адекватности;
k - количество факторов;
fu - число степеней свободы дисперсии воспроизводимости.
Модель считается адекватной, если значение F, полученное по формуле, не превышает соответствующего табличного значения при заданном уровне значимости.
34.Планирование эксперимента. Построение математической модели в натуральных единицах.
Полученные выше регрессионные математические модели являются нормированными, т.к. значения факторов в них могут принимать значения от –1 до +1.
Для практического использования математической модели, удобнее, когда в ней принимают натуральные значения.
Пересчет коэффициентов модели к натуральным значениям факторов производится на основании выражения нормирования факторов

где
 – i-ое
нормированное значение фактора;
– i-ое
нормированное значение фактора;
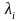 -
i-й
(нижний или верхний) уровень фактора;
-
i-й
(нижний или верхний) уровень фактора;
 -
нулевой уровень фактора;
-
нулевой уровень фактора;
 -
интервал варьирования..
-
интервал варьирования..
Откуда  .
.
35.Планирование эксперимента. Понятие дробного факторного эксперимента. Построение матрицы планирования дробного факторного эксперимента.
С увеличением числа факторов, количество опытов в полном факторном эксперименте резко возрастает. Так при трех факторах необходимо поставить 23 =8 опытов, при восьми – 256 и т.д.
Поэтому целесообразно сократить число опытов за счет информации, которую несут эффекты взаимодействия факторов и которая для построения линейной модели несущественна.
Рассмотрим ПФЭ 22 .
ПФЭ 2к |
№ опыта |
Факторы |
Параметры |
||
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
9 |
|
1 |
+1 |
+1 |
+1 |
Y1 |
22 |
2 |
+1 |
-1 |
+1 |
Y2 |
|
3 |
+1 |
+1 |
-1 |
Y3 |
|
4 |
+1 |
-1 |
-1 |
Y4 |
По нему можно построить модель:
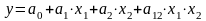 .
.
Однако, если процесс описывается линейной моделью, то достаточно определить только 3 коэффициента: a0; a1; a2, a квадратичный коэффициент а12 будет достаточно малым.
Если включить в матрицу планирования вместо столбца x1x2 фактор х3, то получится матрица планирования для трех факторов, линейная модель которой
 .
.
Коэффициенты
этой модели рассчитываются по формулам,
где коэффициент
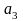 совпадает со значением
совпадает со значением
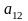 .
.
36.Регрессионный и корреляционный анализ. Обработка результатов натурного и расчетного эксперимента. 248




