25.Понятие агрегата. Основные параметры (множества), характеризующие агрегаты. Описание процесса функционирования агрегата.

Обобщенный (универсальный) подход базируется на понятии агрегативной системы. Она представляет собой формальную схему общего вида, которую называют А – схемой.

При агрегативном описании моделируемый объект (система) декомпозируется на конечное число подсистем с сохранением связей, которые обеспечивают их взаимодействие. В результате декомпозиции, система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, которые объединяются в подсистемы различных уровней. В качестве элемента А – схемы выступает агрегат.

Каждый агрегат A_n, характеризуется:

T – множеством моментов времени

X – множеством входных сигналов

Y – множеством выходных сигналов

Z – множеством состояний

Процессы перехода агрегата из одного состояния в другое происходит за малый промежуток времени, т.е. имеет место скачек состояний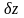 , т.е. переход из состояния z(t₁) в состояние z(t₂) происходит скачком (z(t₂)≠z(t₁)).

Эти переходы определяются собственными (внутренними) параметрами схемы и входными сигналами .

В начальный момент времени t₀ состояние z⁰=z(t₀) задается распределением L[z(t₀)].

Предполагая, что процесс функционирования агрегата в моменты поступления входных сигналов Х_n описываются случайным оператором V:

z(t_n+0)=V[t_n, z(t_n), x_n], где t_n+0 – скачок, t_n – момент поступления входного сигнала.

Процесс функционирования (t_n,t_n+1), t (t_n,t_n+1) описывается случайным оператором :

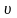z(t)= [t, t_n, z(t_n+0)]

На оператор не накладывалось никаких ограничений, поэтому допустимы скачки состояний в моменты времени, которые не являются моментами поступления входных сигналов. Моменты скачков будем называть особыми моментами времени 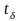, а состояния 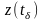- особыми состояниями, тогда:

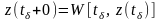
W – частный случай оператора .

На множестве Z выделяется Z^(Y), что если достигает Z^(Y), то это является моментом выдачи выходного сигнала.

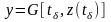, где G – некоторый случайный оператор.

A_n=<T,X,Y,Z, Z^(Y),H,V, ,W,G> - описание отдельного агрегата.

При моделировании реальных систем применяют А-схемы, которые представляют собой конструкции из отдельных агрегатов, связи между ними задаются с помощью оператора сопряжения R.

26.Структура агрегатной системы. Внутренняя и внешняя информация, циркулирующая в а - схемах.

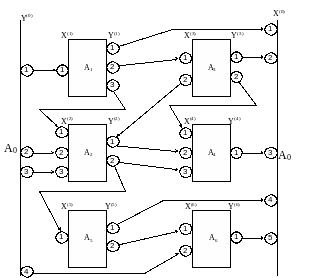
Последовательность входных сигналов, расположенных в порядке их поступления в А – схему называют входным сообщением или X–сообщением.

Последовательность выходных сигналов упорядоченную относительно времени выдачи называют выходным сообщением или Y–сообщением.

Информация, которая циркулирует в А–схеме делиться на внутреннюю и внешнюю. Внешняя поступает от внешних объектов, а внутренняя вырабатывается агрегатами А–схемы.

Обмен информации А–схемы с внешней средой происходит через агрегаты, которые называют полюсами. Различают входные полюсы, на которые поступают X–сообщения и выходные полюсы – это агрегаты, выходная информация которых представляет Y–сообщения.

Каждый агрегат A_n имеет входные к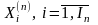онтакты и выходные контакты

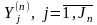
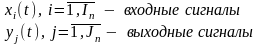
Внешняя среда обозначается фиктивным агрегатом A₀:

Для любого агрегата, включая A₀, можно записать, что агрегат характеризуется множеством входных контактов 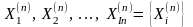и множеством выходных контактов 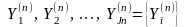, тогда пара 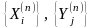представляет математическую модель элемента A_n, которая используется для формального описания сопряжения его с другими элементами А–схемы и с внешней средой.

В силу предположения о независимости передачи сигналов, каждому входному контакту 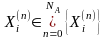соответствует не более чем 1 выходной контакт 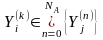, соединенный с ним элементарным каналом .

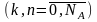Можно ввести однозначный оператор R. 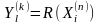, который имеет область определения на множестве 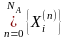и область значений .

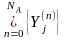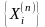
Совокупность множеств и оператор сопряжения R образуют схему сопряжения элементов в систему.

В данном случае это одноуровневая схема сопряжения.

n	i
	1	2	3	4	5
0	1,1	3,1	4,1	5,1	6,1
1	0,1
2	1,3
3	1,2	2,1
4	3,2	2,1	2,2
5	2,2
6	5,2	0,4

n – номер агрегата

i – номер контакта

k – номер элемента

l – номер контакта с которым соединен Х_i⁽ⁿ⁾

k,l – ячейка

Упорядоченную совокупность операторов A_n , агрегата A₀ и оператора R считают А-схемой при следующих ограничениях:

1) Каждый элементарный канал, передающий сигналы во внешнюю среду должен начинаться в одном из выходных контактов одного из агрегатов

А-схемы. Каждый элементарный канал, передающий сигнал из внешней среды должен заканчиваться на одном из входных контактов агрегатов

А–схемы.

2) Сигналы в А–схеме передаются непосредственно от одного агрегата к другому без устройств, которые могут отсеивать сигналы по каким-либо признакам.

3) Необходимо согласование функционирования агрегатов во времени.

4) Сигналы между агрегатами А–схемы передаются мгновенно без перекодирования и исключения сигнала.