5.2. Моделирование постепенных отказов.

Постепенные отказы подчиняются нормальному закону распределения. Интегральная функция нормального закона имеет вид:

где  - среднеквадратичное отклонение; a — математическое ожидание.

Для того, чтобы не рассчитывать интеграл, воспользуемся половинной функцией Лапласа и с ее помощью рассчитаем нормальный закон распределения по формуле:

где Ф(х) - половинная функция Лапласа; х=(t - T_ср)/, где

х - аргумент функции Лапласа;

t - время функционирования;

Т_ср - средняя наработка на отказ;

 - среднеквадратичное отклонение.

На рисунке 4 представлен график половинной функции Лапласа.

Рассчитаем интегральную функцию F(t) нормального распределения для каждого из постепенных износов элементов, определим аргумент функции Лапласа и занесем данные в табл. 5.2 а, б.

Таблица 5.2. а - Сводная таблица расчета интегральной функции нормального распределения для износа резьбовых соединений и пружины.

(=12,909; Т_ср=250000 час).

t∙103, час.	230	235	240	245	250	255	260	265	270
Х	-1,55	-1,16	-0,77	-0,39	0	0,39	0,77	1,16	1,55
Ф(х)	-0,88	-0,75	-0,56	-0,3	0	0,3	0,56	0,75	0,88
F(t)	0,061	0,12	0,22	0,349	0,52	0,65	0,78	0,88	0,94

На основе расчетных данных таблицы 5.2 а построим график нормального распределения (рисунок 5).

Процедура моделирования аналогична рассмотренной выше. Полученную выборку 65 заносим в таблицу 5.3 а.

Полученные в таблице 5.3 а значения сравниваем с Т_ср, т. к. нас интересуют характеристики системы в первый период эксплуатации. В тех случаях, если t₀<T_ср, находим нерабочее время t₀ элемента системы Х₃ по формуле . Полученное время указано в скобках в таблице 5.3. Затем, просуммировав время t₀ по реализации, берем отношение t₀ к суммарному времени функционирования элемента системы Х₃ в этой реализации.

Вероятность отказа элемента системы Х₃ в данной реализации определяем по формуле:

Таблица 5.3 а - Временная выборка из 65 элементов для износа резьбовых соединений и пружины.

m n		Количество элементов						∑t0		∑tобщ		t0/tобщ
		1	2	3	4	5	6
Кол - во реализаций	1	233(17)	239(11)	250	254	261	245(5)		33		1482		0,022
	2	256	243(7)	234(16)	251	256	244(6)		29		1484		0,020
	3	235(15)	230(20)	265	270	264	270		35		1534		0,023
	4	242(8)	263	248(2)	231(19)	265	232(18)		37		1201		0,031
	5	249(1)	267	250	273	238(12)	247(3)		16		1524		0,011

Итого: 0,206

Полный коэффициент отказа элемента системы:

R_X3=0,206/5=0,041

Проведём аналогичное моделирование для остальных резьбовых элементов и пружины: R_Х4, R_Х5, R_Х8.

m n		Количество элементов						∑t0		∑tобщ		t0/tобщ
		1	2	3	4	5	6
Кол - во реализаций	1	236(14)	270	254	263	231(19)	255		33		1509		0,022
	2	246(4)	243(7)	234(16)	261	256	244(6)		28		1484		0,019
	3	235(15)	250	265	254	237(13)	270		28		1511		0,019
	4	242(8)	263	258	241(9)	265	242(8)		25		1511		0,017
	5	249(1)	267	250	270	238(12)	233(17)		30		1507		0,020

Итого:0,097

R_X4=0,097/5=0,019

m n		Количество элементов						∑t0		∑tобщ		t0/tобщ
		1	2	3	4	5	6
Кол - во реализаций	1	246(4)	270	264	253	231(19)	265		23		1529		0,015
	2	246(4)	253	234(16)	261	256	254		20		1504		0,013
	3	235(15)	260	265	250	237(13)	270		28		1521		0,018
	4	242(8)	253	258	241(9)	265	242(8)		25		1501		0,017
	5	249(1)	267	250	270	248(2)	233(17)		20		1517		0,013

Итого:0,076

R_X5=0,076/5=0,015

m n		Количество элементов						∑t0		∑tобщ		t0/tобщ
		1	2	3	4	5	6
Кол - во реализаций	1	246(4)	270	264	253	251	265		4		1549		0,003
	2	245(5)	253	252	261	256	254		5		1524		0,003
	3	235(15)	260	265	250	257	270		15		1541		0,010
	4	242(8)	253	258	241(9)	265	242(8)		25		1501		0,017
	5	249(1)	267	250	270	248(2)	233(17)		20		1517		0,013

Итого:0,046

R_X8=0,046/5=0,009

Таблица 5.2 б - Сводная таблица расчета интегральной функции

нормального распределения для износа резинотехнических изделий

(=25,89; Т_ср=120000 час).

t∙103, час.	80	90	100	110	120	130	140	150	160
Х	-13,2	-12,4	-11,6	-10,8	-10,07	-9,3	-8,5	-7,7	-7
Ф(х)	-0,88	-0,75	-0,56	-0,3	0	0,3	0,56	0,75	0,88
F(t)	0,061	0,12	0,22	0,349	0,5	0,65	0,78	0,88	0,94

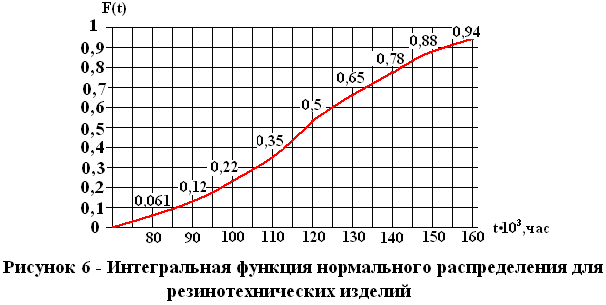
Таблица 5.3 б- Временная выборка из 65 элементов для резинотехнических изделий .

m n		Количество элементов							t0		tобщ		t0/tобщ
		1	2	3	4	5	6
Количество реализаций	1	86(34)	127	106(14)	113(7)	127	142	34		671		0,116
	2	104(16)	101(19)	68(52)	97(23)	150	145	16		665		0,165
	3	91(29)	83(37)	129	92(28)	74(46)	110(10)	29		579		0,259
	4	81(39)	112(8)	155	160	142	140	47		660		0,182
	5	107(13)	100(20)	115(5)	128	149	158	43		658		0,164
Итого: 0,765

R_X9=0,765/5=0,153

m n		Количество элементов							t0		tобщ		t0/tобщ
		1	2	3	4	5	6
Количество реализаций	1	86(34)	127	106(14)	113(7)	167	142	55		741		0,074
	2	104(16)	101(19)	129	159	150	145	35		788		0,044
	3	119(1)	126	127	92(28)	144	167	29		775		0,037
	4	81(39)	112(8)	155	160	142	140	47		790		0,060
	5	107(13)	100(20)	115(5)	128	149	158	38		757		0,051
Итого: 0,266

R_X10=0,266/5=0,053

R_X1= 0,049; R_X2=0,076; R_X3=0,041; R_X4=0,019; R_X5=0,015; R_X6=0,088; R_X7=0,081; R_X8=0,009; R_X9=0,153; R_X10=0,053.

В результате процедуры моделирования получим коэффициенты отказов каждого элемента системы. Рассчитаем коэффициент отказа всей системы, используя формулы для последовательного и параллельного соединения.

для «ИЛИ»

для «И»

Рассчитаем коэффициент отказа системы R_кс по формуле:

R_кс=1 – (1-R_X1) ∙ (1-R_X2) ∙ (1-R_a) ∙ (1-R_X6) ∙ (1-R_X7) ∙ (1-R_b),

где R_a= R_X3∙ R_X4∙ R_X5 = 0,041∙0,019∙0,015= 0,000012

R_a= R_X8∙ R_X9∙ R_X10= 0,009∙0,153∙0,053=0,000072

Отсюда:

R_кс=1 – (1-0,049) ∙ (1-0,076) ∙ (1-0,000012) ∙ (1-0,088) ∙ (1-0,081) ∙ ∙(1-0,000072)=1-0,951∙0,924∙0,999988∙0,912∙0,919∙0,999928 = 0,26.