3.Рачет надежности вентиля запорного

3.1. Анализ надёжности и износа элементов деталей конструкции.

Количественной мерой надежности деталей и машин является величина вероятности безотказной работы, определяемая на основе статистических закономерностей.

Характеристики прочности по соответствующим критериям и напряженности деталей машин подвержены рассеянию и, являясь случайными величинами, могут быть отображены различными законами распределений. Отказы делятся на внезапные и постепенные. Внезапные отказы технических элементов подчиняются экспоненциальному закону распределения, а постепенные — нормальному. Примером внезапных (В) отказов являются поломка, обрыв, излом, а постепенных (П) — износ, старение, усталостный износ.

Для количественной оценки надежности запорного вентиля системы водоснабжения приведем схему устройства (рисунок 1.1).

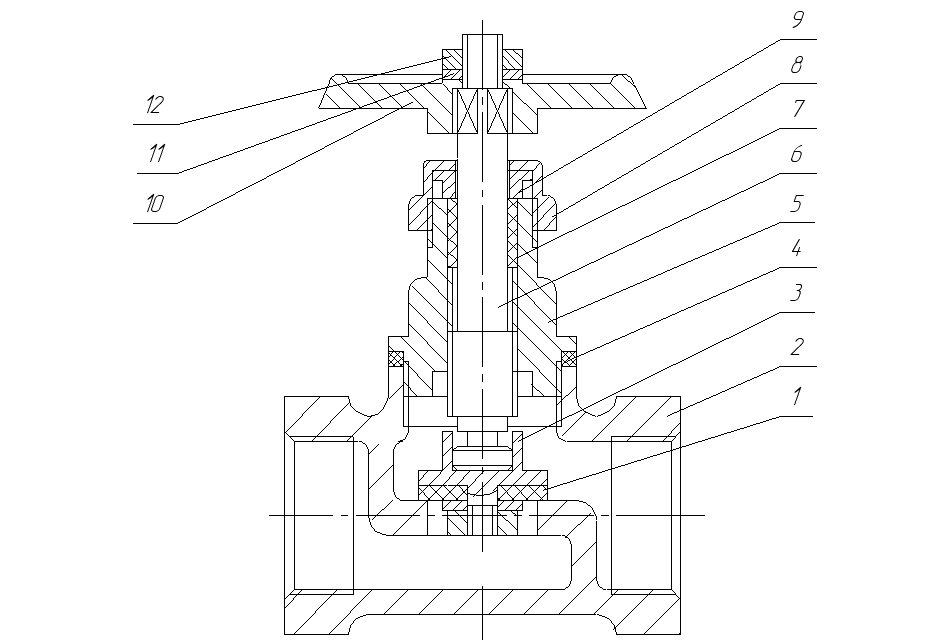
Рисунок 1.1 - Вентиль запорный: 1 - прокладка, 2 – корпус, 3 - золотник, 4, 7 – уплотнительная прокладка, 5 - втулка, 6 - шпиндель, 8 - гайка, 9 – втулка, 10 - маховичек, 11 - шайба, 12 - гайка

Условимся все устройства называть системой, а составные части — ее элементами. Определим, какие элементы подвержены внезапному отказу, какие — постепенному. Обозначим отказы элементов устройства через Х₁, Х₂, Х_З, …, Х_n (рисунок 1.2) и определим тип отказа.

X₁ -износ (разрушение) главных входных и выходных

элементов вентиля (В);

Х₂ -износ прокладки (П);

Х_3, Х_4, X_5, X₆ - износ резьбовых соединений (П);

Х₇, Х₈ - износ гаек (П);

Х₉ - износ шпинделя (П);

Х_10, Х₁₁ - износ уплотнительные прокладки (П);

Рисунок 1.2 – Обозначения отказов элементов

2. Структурная схема надёжности и дерево отказов элементов

деталей конструкции.

Элементы, имеющие высокую степень надежности и отказы, имеющие малую вероятность появления, не учитываются логико-вероятностным методом и не включаются в структурную схему надежности.

Построим структурную схему надежности механической системы в виде последовательных и параллельных соединений (рисунок 1.3).

X₂

X₃

X₆

X₄

X₁

X₅

X₈

X₇

X₉

X₁₀

X₁₁

Рисунок 1.3 - Структурная схема надежности механической системы

Составим на основе структурной схемы «дерево отказов» (рисунок 3.4), используя правило Моргана, когда последовательное соединение элементов в логической структуре «дерева» соединяется логическим знаком «ИЛИ», параллельные соединения — знаком «И».

КС

R_а

R_в

Х₁

Х₂ Х₃ Х₄ Х₅ Х₇ Х₉ Х₁₀ Х₁₁

Х₆ Х₈

Рисунок 1.4 - «Дерево отказов»

2. Моделирование отказов элементов устройства.

1. Моделирование внезапных отказов.

Построим интегральную функцию экспоненциального распределения:

(2.1)

где  — интенсивность отказов.

Интенсивность отказов главных входных и выходных элементов запорного вентиля:

(2.2)

где Т_ср — среднее время наработки на отказ.

Примем среднюю наработку на отказ устройства Т_ср=200000 часов.

F(20000)=0,01	F(140000)=0,50
F(40000)=0,18	F(200000)=0,63
F(60000)=0,26	F(300000)=0,78
F(100000)=0,39	F(350000)=0,83

По расчетным данным построим интегральную функцию экспоненциального распределения. На оси абсцисс отложим время t в 34 раза больше Т_ср. На оси ординат — значение функции F(t).

На основе метода «Монте-Карло» промоделируем вероятность случайных отказов. Выбрасываем с помощью генератора случайных чисел числовую последовательность R в диапазоне значений (01).

Отложим каждое из чисел числовой последовательности R по оси ординат (например: 0,9), проведем прямую, параллельную оси абсцисс (см. рисунок 2.1) до пересечения с графиком функции F(t) и из точки пересечения опустим перпендикуляр на ось времени; таким образом, получаются значения времени, соответствующие каждому числу последовательности, приведенные в первой строчке таблицы 2.1, которые называются реализацией времени функционирования устройства. Таких реализаций получим не менее 5 (1, 2, 3, 4, 5 строчки таблицы). Набор реализаций называется выборкой из 65 элементов.

F(t)

t, час

Рисунок 2.1 - Интегральная функция экспоненциального распределения входных и выходных элементов, =510^-6, 1/час.

Таблица 2.1. Временная выборка из пяти реализаций для входных и

выходных элементов.

m n		Количество элементов							t0		tобщ		t0/tобщ
		1	2	3	4	5	6
Количество реализаций	1	20(80)	71(29)	140	183	322	460	109		1196		0,091
	2	365	47(53)	209	256	37(63)	58(42)	158		972		0,163
	3	98(2)	669	38(62)	59(41)	345	22 (78)	183		1231		0,149
	4	432	100	38(62)	211	368	346	62		1495		0,041
	5	14(86)	58(42)	74(26)	327	475	538	154		1486		0,104
Итого: 0,548

Далее временные значения t_i, приведенные в таблице 2.1, сравниваем с Т_ср/2, поскольку нас интересует поведение системы в первый полупериод эксплуатации. Затем получим время t₀ нерабочего состояния элемента системы Х₁, выбирая лишь те случаи, когда t_i<Т_ср/2. Расчет производится по формуле

(2.3)

Полученное значение t₀ заносим в таблицу 2.1, указав его в скобках, затем суммируем нерабочее время в единичной реализации t₀ и берем отношение к сумме общего времени t_общ работы элемента в этой реализации. На основе полученных значений определим вероятность отказа элемента системы Х₁ для данной реализации по формуле:

(2.4)

и так для каждой реализации.

Вероятность отказа элемента системы Х₈ является средним арифметическим этих значений:

(2.5)